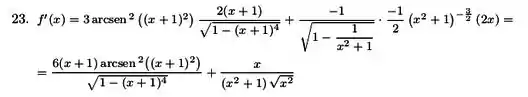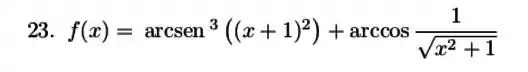
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivadas de Funções Inversas Trigonométricas

Ver Teoria
Exercício 5212345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505153545556575859606162636465

Enunciado

Passo 1

Vamos aplicar a Regra da Cadeia nessa função:

g ' x = arcsen 3 ⁡ x + 1 2 + arccos ⁡ 1 x 2 + 1 '

Regra da Cadeia no primeiro termo, é um x + 1 2 dentro do arco seno, que é como se estivesse dentro de um x 3 , já que está elevado ao cubo.

= 3 arcsen 2 ⁡ x + 1 2 1 1 - x + 1 2 2 x + 1 2 ' + - 1 1 - 1 x 2 + 1 2 1 x 2 + 1 '

= 3 arcsen 2 ⁡ x + 1 2 1 1 - x + 1 4 2 x + 1 + - 1 1 - 1 x 2 + 1 - x 2 + 1 ' 2 x 2 + 1 3 2

= 2 x + 1 3 arcsen 2 ⁡ x + 1 2 1 - x + 1 4 + - 1 x 2 + 1 - 1 x 2 + 1 - 2 x 2 x 2 + 1 3 2

Passo 2

A partir daqui, tudo se resume a usar recursos matemáticos para tornar essa expressão melhorzinha:

= 2 x + 1 3 arcsen 2 ⁡ x + 1 2 1 - x + 1 4 + 1 x 2 x 2 + 1 x x 2 + 1 3 2

= 6 x + 1 arcsen 2 ⁡ x + 1 2 1 - x + 1 4 + x 2 + 1 x 2 x x 2 + 1 3 2

= 6 x + 1 arcsen 2 ⁡ x + 1 2 1 - x + 1 4 + x 2 + 1 1 2 x 2 x x 2 + 1 3 2

= 6 x + 1 arcsen 2 ⁡ x + 1 2 1 - x + 1 4 + x x 2 x 2 + 1

Resposta

Exercícios de Livros Relacionados

Resolva o exercício 54 da série de exercícios 8.1, mostrando que arctan ⁡ x e - arctan ⁡ 1 x diferem por uma constante e então calcule-a.
Dois pontos, A e B , são diametralmente opostos nas praias de um lago circular com 1 km de diâmetro. Uma pessoa deseja ir do ponto A ao ponto B . Ela pode remar a uma velocidade de 1 1 2 km/h e andar
Encontre a derivada da função dada:f (x) = sec^(- 1) (sqrt(x^2 + 4))
Encontre a derivada da função dada:f (x) = ln (tg^(- 1) 3 x)
Encontre a derivada da função dada:g (x) = x^2 sec^(- 1) (1)/(x)