2) Seja
Considere
- Mostre que a função é inversível em todo o seu domínio
- Determine a equação da reta tangente ao gráfico de (a inversa de ) em . Dica: não é necessário determinar
- Determine o domínio de e uma expressão para
Passo 1
Bem, pelo enunciado já deu pra ver que vamos usar o Teorema da Função Inversa o tempo todo né? Uma coisa maneira que o TFI diz pra gente é o seguinte
Bem, é derivável! Afinal, é uma função contínua. Sua derivada vai ser:
Agora, da uma olhada só o circula trigonométrico:
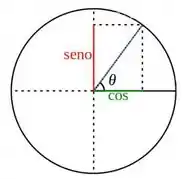
Como o domínio é:
Estamos falando do segundo quadrante! Mas como temos e não , qualquer dentro do domínio que a gente inserir, vai dar um valor de seno de algum arco do terceiro ou quarto quadrante. Em outras palavras:
Como esses quadrantes estão na parte de baixo do círculo trigonométrico, todos os valores de seno serão negativos! Sendo assim da pra afirmar com certeza que:
O que é, por si só, prova o suficiente de que é inversível em todo o seu domínio! Uhuul
Passo 2
Agora vamos complicar um tico mais. Estamos falando de reta tangente na letra . Mas ó! Tangente a inversa de ! O primeiro passo vai ser modelar a equação. Vamos ter:
Onde é o ponto de tangência e é o coeficiente angular da reta. Veja bem, o enunciado já dá pra gente o ponto de tangência ao dizer que ! Sendo assim:
Bora lá terminar essa modelagem. Vamos supor que sabemos o valor de . Esse valor vai ser:
Oras, como essa é a inversa de , podemos afirmar também:
Já que uma função inversa tem domínio e contra domínio trocados de lado em relação a sua função original. Como sabemos a expressão de , da pra gente achar o valor de
Cosseno zerando? Bora olhar o círculo trigonométrico de novo
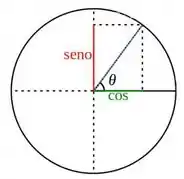
Com o domínio é e pertence ao domínio podemos afirmar que:
O único arco que zera o cosseno nesse intervalo, é o de . Da pra ver isso direitinho no círculo. Sendo assim:
Agora que sabemos o valor de , sabemos então que:
E logo a equação da reta tangente fica:
Pra fechar com chave de ouro, basta a gente achar o coeficiente angular. Pra isso precisamos usar o a fórmulinha do teorema da derivada da função inversa, que é esse aqui ó:
Aplicando , temos:
A derivada de a gente já fez, não é mesmo? Isso vai dar:
Fechou então, a equação da reta tangente será:
Passo 3
Lembra que a gente falou que uma função inversa tem domínio e contra domínio trocados de lado em relação a sua função original. Então o dóminio vai ser:
Pra achar a imagem de a gente só precisa achar todos os valores de que a função pode assumir. Mas olha que sagaz, como:
Então é decrescente em seu domínio! Oras, seu maior então ocorre em e seu menor ocorre em . Vamos ter:
A imagem de vai ser então:
Passo 4
Quanto a uma expressão de ? Vamos pensar no seguinte, vamos estabelecer que
Onde . Como sabemos os valores possíveis de , podemos estabelecer domínio e imagem de :
Onde a primeira coluna é o domínio e a segunda a imagem. Com dúvidas de que isso ta certo? Tente substituir:
Pra fazer a função inversa de , basta trocarmos domínio com contra domínio:
Mas qual será a expressão de ? Bem, como eu estou fazendo função inversa, com certeza um vai aparecer. Mas será que é o suficiente escrever ? O que terá no lugar da bolinha ? Terá mais alguma coisa. Bom, vamos fazer um primeiro teste:
Ta errado né? O resultado que deveríamos achar era:
Ai sim estaríamos respeitando a imagem de . Vamos fazer o seguinte, já que nem nem devem dar , vamos somar a expressão, logo teremos:
Opa, tamos chegando perto em! Se dividirmos tudo por então vamos ficar
E pra fechar com chave de ouro, como e estão trocados de lugar, basta só negativar o . A inversa correta será:
Concluímos que:
Ok ok, mas como isso ajuda a gente? Não é que eu quero e sim ! Bem, como eu quero a inversa de , tenho que arranjar uma forma de escrever:
Afinal de contas se eu inverter essa equação vou ter:
Bem, como eu sei que:
Só escrevendo no lugar de , tenho o seguinte resultado:
Opa, a inversa de em função de eu já conheço! Invertendo como fizemos com agora a pouco conseguimos a seguinte relação:
Agora é só pegar a expressão de e todo lugar onde o aparece trocar ele por . Vamos ficar com:
E finalmente, como , chegamos ao nosso final feliz:
Pra fins visuais, toda inversa de uma função é igual ao espelho da função original em relação ao eixo . Saca só que bacana:
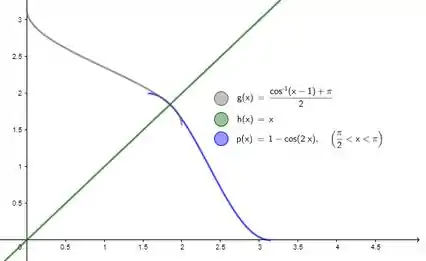
Resposta
- A função possui uma inversa uma vez que ela é derivável e pelo TFI basta para ter inversa.