![]()
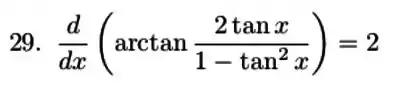
Passo 1
Vamos aplicar a Regra da Cadeia nessa função:
Isso será, pela Cadeia, a derivada de , , com o no lugar desse , multiplicado pela derivada do próprio .
Passo 2
A partir daqui, só temos que dar uma arrumada na expressão.
Uso no denominador o produto notável do quadrado da soma
Mas aqui tem uma propriedade trigonométrica pra gente usar:
Com isso,
Passo 3
Agora, tem um jeito mais inteligente de fazermos essa questão. Sabe o termo dentro do arco tangente?
Esse cara é exatamente a forma trigonométrica de se calcular a tangente do dobro de , ou seja:
Com isso, olha a função, fica assim:
O arco tangente é a função inversa da tangent, certo? E repara, se temos a função aplicada composta com a sua inversa, temos a seguinte propriedade:
Ou seja, sabe quem é ? Isso aqui:
Com isso, a derivada é:
Bem mais elegante, né?