Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivadas de Funções Inversas Trigonométricas

Ver Teoria
Exercício 6112345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596062636465

Enunciado

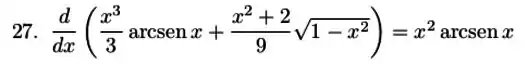
Passo 1

Para verificar a igualdade

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x

O que a gente precisa fazer é derivar isso que está dentro do parenteses em relação a x e ver se achamos a mesma coisa que tem do lado direito dessa equação.

Passo 2

Usando a regra do produto para derivar a primeira parte e a regra do produto e da cadeia para derivar a segunda parte, temos

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = 3 x 2 3 arcsen ⁡ x + x 3 3 1 1 - x 2 + 2 x 9 1 - x 2 + x 2 + 2 9 ∙ 1 2 1 - x 2 ∙ - 2 x  

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + x 3 3 1 - x 2 + 2 x 1 - x 2 9 - x ( x 2 + 2 ) 9 1 - x 2

Passo 3

Rearrumando isso pra facilitar a visualização:

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x 1 - x 2 9 + x 3 3 1 - x 2 - x 3 + 2 x 9 1 - x 2

Agora, fazendo o mmc das duas ultimas frações:

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x 1 - x 2 9 + 3 x 3 - x 3 - 2 x 9 1 - x 2

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x 1 - x 2 9 + 2 x 3 - 2 x 9 1 - x 2

Fazendo de novo o mmc:

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x 1 - x 2 ∙ 1 - x 2 9 1 - x 2 + 2 x 3 - 2 x 9 1 - x 2

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x 1 - x 2 9 1 - x 2 + 2 x 3 - 2 x 9 1 - x 2

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x - 2 x 3 9 1 - x 2 + 2 x 3 - 2 x 9 1 - x 2

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x + 2 x - 2 x 3 + 2 x 3 - 2 x 9 1 - x 2

Ou seja,

d x 3 3 arcsen ⁡ x + x 2 + 2 9 1 - x 2 d x = x 2 arcsen ⁡ x

Igualdade verificada

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Resolva o exercício 54 da série de exercícios 8.1, mostrando que arctan ⁡ x e - arctan ⁡ 1 x diferem por uma constante e então calcule-a.
Dois pontos, A e B , são diametralmente opostos nas praias de um lago circular com 1 km de diâmetro. Uma pessoa deseja ir do ponto A ao ponto B . Ela pode remar a uma velocidade de 1 1 2 km/h e andar
Encontre a derivada da função dada:f (x) = sec^(- 1) (sqrt(x^2 + 4))
Encontre a derivada da função dada:f (x) = ln (tg^(- 1) 3 x)
Encontre a derivada da função dada:g (x) = x^2 sec^(- 1) (1)/(x)