
Passo 1
Vamos começar interpretando essa primeira frase do enunciado aí:
A distância de um ponto ao eixo pode ser dado por Pitágoras:
Então a densidade, em termos “matemáticos” é essa distância vezes uma constante de proporcionalidade que vamos chamar de , assim
E sabemos que a massa de um sólido pode ser dada por
Vamos tentar visualizar o nosso solido agora então, temos a região entre dois cilindros, embaixo do cone e em cima de .
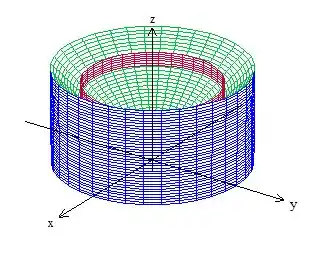
É válido lembrar que, a ideia de um esboço na sua prova é te ajudar a identificar a região de integração! Ou seja, se você não conseguir fazer o desenho na hora, tenta esboçar qualquer coisa que te ajude a visualizar =D
Nessa questão aqui se o esboço estiver muito complicado, tenta ver alguma coisa parecida no que geralmente é mais simples, tipo isso aqui
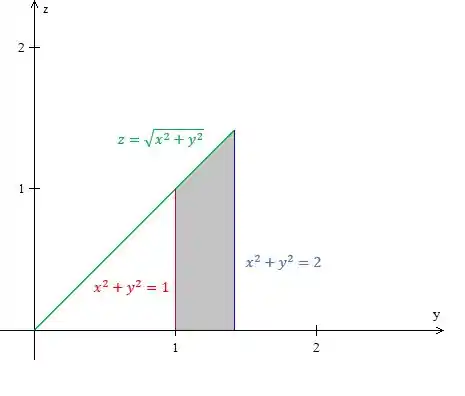
Com esse esboço mais simples, dá pra ver que a região de interesse está com entre e o cone, logo
E estão entre os cilindros, logo
Passo 2
Pra facilitar nosso trabalho aqui, vamos escrever tudo isso em coordenadas cilíndricas, pra isso:
Aplicando nos limites que temos:
Agora em
Como temos o cilindro dando a volta completa no espaço, os limites de são
Pra fechar, só falta a gente escrever a densidade em coordenadas cilíndricas também
Assim, não se esquecendo de multiplicar tudo pelo jacobiano , temos
Passo 3
Começando pela integral em
Integrando em
Por fim, integrando em