Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 15123456789101112131416171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Ache a massa do sólido limitado pelas superfícies z = x 2 + y 2 , 2 z 2 - x 2 - y 2 = 4 com densidade δ x , y , z = z

Passo 1

Para calcular a massa vamos precisar da seguinte integral:

M = ∭ W δ x , y , z d V

Vamos então ter que descobrir os limites de integração de W , certo? O esboço é esse aqui:

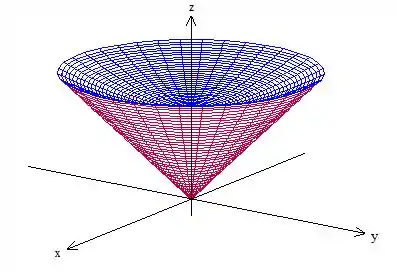
Onde a superfície vermelha é o cone z = x 2 + y 2 e a azul é 2 z 2 - x 2 - y 2 = 4 que podemos reescrever da seguinte forma:

z = 4 + x 2 + y 2 2

Então os limites de z são:

x 2 + y 2 ≤ z ≤ 4 + x 2 + y 2 2

Passo 2

Nosso limite tem muito x 2 + y 2 , né? Vamos fazer uma mudança para coordenadas cilíndricas para ver se fica melhor:

x = r cos ⁡ θ

y = r sen ⁡ θ

z = z

J = r

Os novos limites de z vão ser

r ≤ z ≤ 4 + r 2 2

Beleza, e como vamos achar os limites de r e θ ? Vemos pelo gráfico que r varia de zero até a interseção das superfícies, então, igualando as duas ficamos com

r = 4 + r 2 2 → 2 r 2 = 4 + r 2

r = 2

Logo

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

Passo 3

Definidos os limites, vamos voltar para a nossa integral de massa

M = ∭ W δ x , y , z d V = ∫ 0 2 π ∫ 0 2 ∫ r 4 + r 2 2 ( z r ) d z d r d θ

Passo 4

Integrando em z

= ∫ 0 2 π ∫ 0 2 r z 2 2 z = r z = 4 + r 2 2 d r d θ = 1 2 ∫ 0 2 π ∫ 0 2 r 4 + r 2 2 - r 2 d r d θ

= 1 2 ∫ 0 2 π ∫ 0 2 2 r - r 3 2 d r d θ

Integrando em r

= 1 2 ∫ 0 2 π 2 r 2 2 - r 4 8 r = 0 r = 2 d θ

= 1 2 ∫ 0 2 π 4 - 2 d θ = ∫ 0 2 π d θ

Integrando em θ

= 2 π

Resposta

M = 2 π

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )