USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 31a
Calcule onde R é limitada por:
- , , para
Passo 1
Olá meu caro amigo, agora é hora de colocar a mão na massa e resolver uma bela integral tripla. Iremos antes de tudo dar uma olhada na carinha da região R e depois vamos pensar em alguma parametrização interessante.
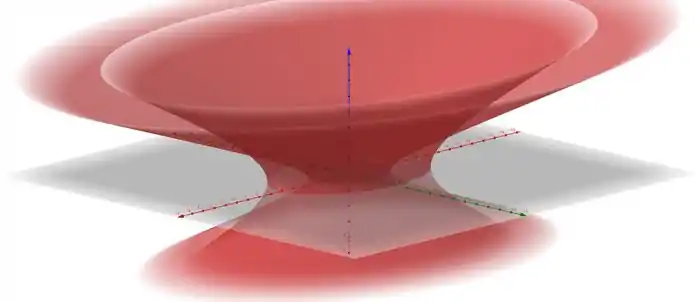
A região R �� essa ai, com um adicional que queremos apenas a parte , então apenas a parte de cima.
Passo 2
Uma parametrização legal para usarmos é a seguinte
E o nosso querido jacobiano é
Os limites de integração iremos descobrir com a parametrização
Como queremos apenas
Passo 3
Hora de montar e calcular a integral
Resposta
Exercícios de Livros Relacionados
Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )