Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 23123456789101112131415161718192021222425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Seja o volume do sólido W comum às esferas x 2 + y 2 + z 2 = 1 e x 2 + y 2 + z 2 = 2 z . Expresse (sem calcular) o volume de W em coordenadas cilíndricas na ordem d z d r d θ .

Passo 1

Vamos, então, fazer um esboço das esferas para entender melhor o que está sendo pedido:

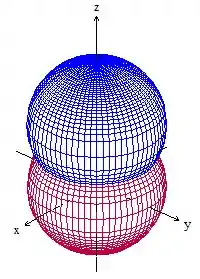
A parte que é interna às duas esferas vai ficar entre as duas calotas. Olha como fica a região W

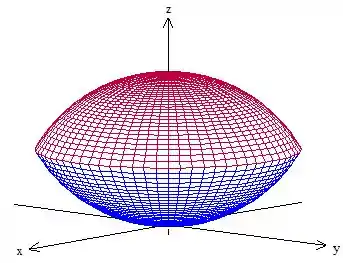
Passo 2

Vamos escrever em coordenadas cilíndricas

x = r cos ⁡ θ

y = r sen ⁡ θ

z = z

J = r

Passo 3

Pelo gráfico, podemos ver que 0 ≤ θ ≤ 2 π . Para descobrir o intervalo de integração primeiro vamos ver onde as esferas se cruzam.

x 2 + y 2 + z 2 = 1

x 2 + y 2 + z 2 = 2 z

Vamos ter

2 z = 1

z = 1 2

Como fica a equação onde as esferas se cruzam.

x 2 + y 2 + 1 2 2 = 1

x 2 + y 2 = 1 - 1 4

x 2 + y 2 = 3 4

Essa é uma equação de uma circunferência de raio r = 3 4 = 3 2 , portanto, descobrimos que 0 ≤ r ≤ 3 2

Falta agora descobrirmos o valor de z , repara que ele vai de uma esfera até a outra. Então z vai da esfera

x 2 + y 2 + z 2 = 2 z

Vamos completar quadrados antes

x 2 + y 2 + z 2 - 2 z = 0

x 2 + y 2 + z - 1 2 = 1

Substituindo as coordenadas cilíndricas

r cos ⁡ θ 2 + r sen ⁡ θ 2 + z - 1 2 = 1

r 2 + z - 1 2 = 1

z - 1 2 = 1 - r 2

Como queremos a parte de baixo dessa esfera, vamos ter

z - 1 = - 1 - r 2

z = 1 - 1 - r 2

Vamos ver agora o limite superior para z , que vai ser a outra esfera

x 2 + y 2 + z 2 = 1

Substituindo as coordenadas cilíndricas

r cos ⁡ θ 2 + r sen ⁡ θ 2 + z 2 = 1

r 2 + z 2 = 1

z 2 = 1 - r 2

Como queremos a parte de cima dessa esfera, vamos ter

z = 1 - r 2

Podemos escrever a região W como

W = r , θ , z 0 ≤ r ≤ 3 2 ,   0 ≤ θ ≤ 2 π , 1 - 1 - r 2 ≤ z ≤ 1 - r 2

Passo 4

A integral do volume vai ficar

V o l W = ∫ 0 2 π ∫ 0 3 / 2 ∫ 1 - 1 - r 2 1 - r 2 r d z d r d θ

Resposta

V o l W = ∫ 0 2 π ∫ 0 3 / 2 ∫ 1 - 1 - r 2 1 - r 2 r d z d r d θ

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )