Calcule o volume do sólido , sabendo que é a região contida em cujos pontos satisfazem e , sendo uma constante maior que zero.
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido.
A equação se refere a uma esfera de raio .
Vamos agora analisar a expressão . Perceba que ela deve ser dividida em duas, pois, se:
- , temos e a equação se torna . Após completar o quadrado, vemos que é a equação de um cilindro de raio centrado em
- , temos e a equação se torna . Essa é a equação de um cilindro que também possui raio , mas está centrado em
Então, a região do problema será representada assim:
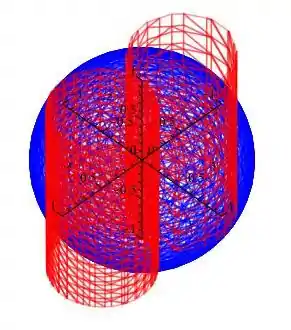
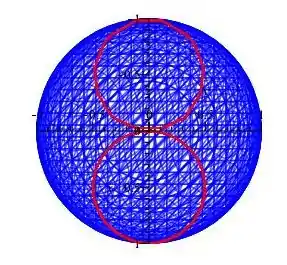
A região vista de cima.
Note que essa região pode ser dividida em partes de volumes iguais, cada uma delas em um octante. Então, vamos calcular o volume da região contida no (onde ) e multiplicar por . Chamaremos essa região de .
Passo 2
Agora precisamos descrever matematicamente essa região , certo? Em coordenadas cartesianas isso parece um pouco complicado, então, como temos um cilindro e as equações que delimitam possuem termos quadráticos, vamos tentar as coordenadas cilíndricas. Faremos:
Passo 3
Vamos, agora, descobrir os intervalos de integração. Fazendo essa substituição na equação da esfera, temos:
Como estamos nos referindo apenas ao 1º octante, temos
Pelo próprio gráfico, já vemos que (o que equivale a de circunferência). Resta, agora, descobrir o intervalo de . Para isso, vamos fazer a substituição cilíndrica na equação do cilindro :
Esse termo “” apareceu porque o cilindro não está centrado na origem, como os que vimos até agora, então, a distância da sua superfície ao eixo varia de acordo com .
Os valores de variam desde a superfície do cilindro até a da esfera, certo? Então temos , mas qual o seu valor máximo? Perceba que para qualquer ângulo , a esfera tem como distância máxima até o eixo , exatamente seu raio. Podemos ver isso fazendo sua interseção com o plano , onde seu raio é máximo:
A região será, então, escrita como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Integrando em relação a , temos:
Passo 6
Fazendo a substituição , temos e a integral passa a ser:
Passo 7
Essa integral pode ser rearrumada como:
Agora, se fizermos a substituição , temos e a integral passa a ser: