Usando uma integral tripla, calcule o volume do sólido delimitado pelas superfícies e .
Passo 1
Eita, questão de integral tripla? Enrolado né? Mas calma gafanhoto, vamos tirar de letra. Pra começo de conversa, vamos olhar as superfícies:
Conhecer os tipos de superfície aqui ajudam muito a gente. Veja que na primeira equação, quando colocamos temos a equação de um círculo no plano e quando colocamos e , a de uma elipse nos planos e respectivamente. Sendo assim, a primeira equação nada mais é do que um elipsoide:
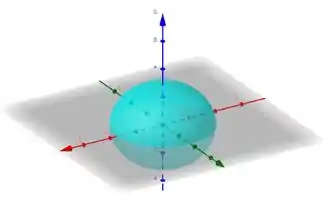
Já pra segunda equação, quando fazemos , ficamos um uma equação de um círculo de raio zero, logo, temos a origem!. Ao fazermos e , achamos equações de parábolas nos planos e respectivamente. A segunda equação vai ser então de um paraboloide:
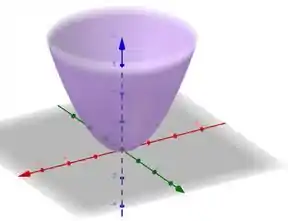
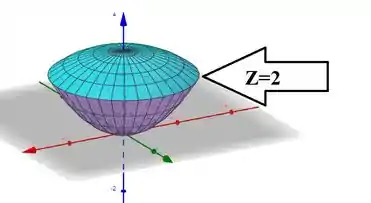
E a interseção desses dois carinhas vai ser mais ou menos assim:
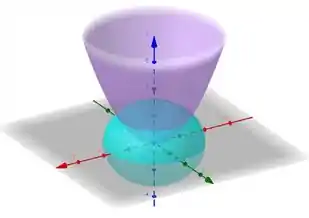
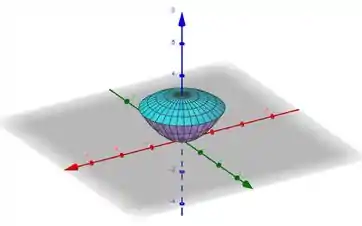
Olhando pra cara desse sólido, vemos que uma boa ideia é usar coordenadas cilíndricas! Afinal, se fizermos:
A equação do elipsoide vira:
Escrevendo e considerando que já sabemos que porque não consideramos todo elipsoide mesmo, temos:
E pro paraboloide, a equação fica:
Como o sólido está definido entre o paraboloide e o elipsoide, vamos ter:
E o volume do sólido será:
Onde o que surgiu dentro da integral é o Jacobiano da mudança pra coordenadas cilíndricas, os limites de integração são os intervalos de encontrados e é a região de integração projetada sobre o plano , que vamos ver agora!
Passo 2
Galera, a região de integração tem que ser pensada de forma a gente ver direitinho os intervalos de integração pras variáveis e , que é o que falta. Se pensarmos que as superfícies tem as seguintes equações:
Vemos que uma boa ideia pra entender qual a região é colocar a segunda equação inteiramente dentro da primeira. Saca só:
Opa, um polinômio do segundo grau! Sendo então
Calculamos:
Como , temos que:
E galera, essa é a altura em que as superfícies se tocam:
Qual vai ser a interseção delas? Bem, eu posso usar o dentro da equação de qualquer uma delas pra entender isso. É mais rápido se eu jogar dentro da equação do paraboloide:
E povo! Olha que bacana, isso nada mais é do que a equação de um círculo de raio ! A gente pode ainda achar matematicamente esse raio se pegarmos a equação do paraboloide em coordenadas cilíndricas:
Portanto, já temos a variação dos outros parâmetros:
Onde varia assim porque estamos considerando o sólido inteiro, e não só um quarto de volta dele, meia volta dele, etc. O volume fica:
Veja que já podemos simplificar essa fórmula um pouco antes de começar as contas, afinal, isso é o mesmo que:
E como dentro de não tem nenhum termo de , aos olhos da integral mais externa, isso nada mais é do que uma graaaandíssima constante. Ou seja:
Show, vamos então pro próximo passo terminar essa integração ai!
Passo 3
Temos então:
Vamos integrar quem tá dentro primeiro. Aos olhos de uma integral , o é uma constante! Então vamos ter:
Pra facilitar a vida, podemos separar essa integral em duas, dessa forma ó:
Assim, resolvendo a mais simples primeiro, temos:
E pra mais complicada, temos que fazer uma substituição simples:
A integral se transforma em:
Integrando, temos:
Juntando tudo, temos:
Feshow!