UFF – Cálculo 2 – P2 – Questão 3
Calcule o sólido limitado por limitado pelo paraboloide pelo plano
Passo 1
Oi, tudo bem? Vou te ajudar a resolver esse problema, vamos lá? O problema pediu para calcular o volume do sólido compreendido pelo paraboloide
E limitado pelo plano
Como temos duas coordenadas ao quadrado e uma linear, vamos usar coordenadas cilíndricas! (se fossem todas coordenadas ao quadrado, usaríamos esféricas). Em coordenadas cilíndricas essas duas equações ficam assim
Podemos fazer um esboço dessa região:
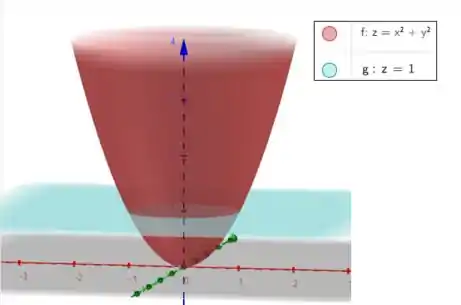
Agora sabemos que embaixo temos o paraboloide e por cima temos o plano limitando superiormente
E as outras coordenadas? Quando , temos que
Temos um círculo de raio , ou seja
E queremos por toda volta
Tranquilo até aqui?
Então a ideia aqui é usar os limites que acabamos de definir na integral do volume em cilíndricas
Bora começar?
Passo 2
Nosso volume é
E o diferencial de volume em cilíndricas é
Tudo bem até aqui? Agora vamos montar nossa integral tripla
beleza?
Passo 3
Agora é #partiu resolver! Começando em
Beleza?
Agora em
E por fim em
Ufa! Terminamos!
Até a próxima!