Determine o volume do sólido entre os cilindros e e os cones e
Passo 1
Ele quer o volume desse sólido, vamos chamar esse sólido de , o volume vai ser
Vamos entender como é esse sólido agora.
Temos dois cilindros, então o sólido vai ser entre os dois cilindros que ele deu.
O detalhe é como vai ser a tampa dessa parada.
Repara que é sempre positivo, porque é uma raiz quadrada, e é sempre negativo porque tem aquele menos ali.
Então podemos dizer que vai do cone negativo ao cone positivo. Vamos ver como fica o gráfico dessa parada
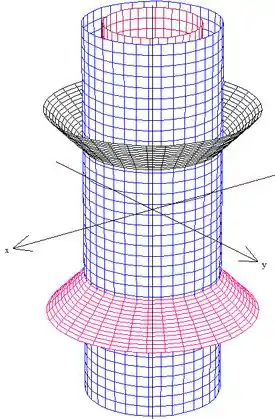
Passo 2
Como esse sólido tem simetria em relação ao eixo e temos dois cilindros bonitinhos com um monte de termos quadráticos, vamos usar coordenadas cilíndricas. Teremos
Passo 3
Temos que descobrir agora os limites de integração. Primeiro, já vimos que ele vai de um cilindro ao outro, então o raio vai do raio de um desses cilindros até o outro. As fórmulas dos cilindros são
Então
Já vimos que vai do cone negativo ao positivo, falta substituir os valores de e nessas equações
Como é sempre positivo por definição, teremos
Falta achar . Repara que o sólido está envolto no eixo , então demos uma volta completa. Assim
O sólido vai ser
Passo 4
Vamos agora montar nossa integral
Resolvendo essa integral temos