Coordenadas cilíndricas
Calcule o volume da região dada por e .
Passo 1
O volume do sólido é dado por:
Onde é limitada por uma hiperboloide de uma folha e por um cone deslocado da origem:
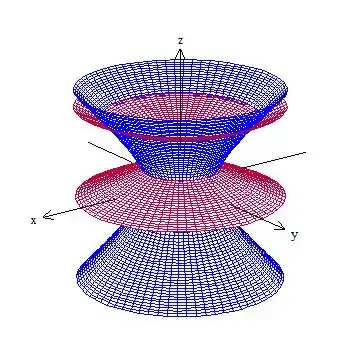
Fazendo os cortes, temos o seguinte:
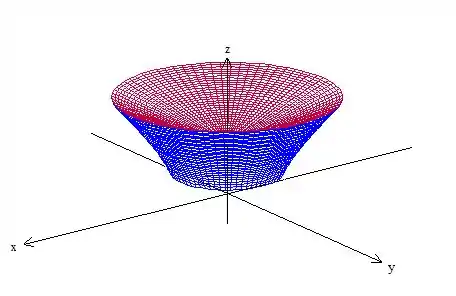
Passo 2
Beleza, agora precisamos escrever essa região de integração. Temos um cone e um hiperboloide, ambos com termos e nas equações, o que nos faz pensar em coordenadas cilíndricas.
Fazendo a mudança no cone, temos:
Para o hiperboloide:
Como o raio fica entre o cone e o hiperboloide, temos .
Como temos uma volta completa em torno do eixo , . Agora falta o intervalo de .
Pela figura, percebemos que as superfícies se cortam duas vezes. Vamos fazer a interseção entre suas equações para descobrir onde isso ocorre:
Então, .
Podemos escrever a região como:
Passo 3
Vamos agora substituir os intervalos que encontramos na integral:
Passo 4
Integrando em relação a , temos:
Passo 5
Agora em relação a :
Passo 6
Finalmente, em relação a :