Stewart, James. Cálculo, volume 2, ed 7ª – Capítulo 15 – Seção 7 – Questão 18
Calcule a integral tripla.
Onde é limitado pelo cilindro e pelos planos , e no primeiro octante.
Passo 1
Fala ai, galerinha bonita! Todos prontos para mais uma integral tripla? Nesse exercício famos resolver a integral:
E como o enunciado não nos deu diretamente os intervalos de integração, vamos olhar para as limitações do volume .
A equação
representa um círculo no plano , onde é uma constante qualquer, já que a equação não depende de , então é como de pegássemos a circunferência e esticássemos ela de menos infinito até mais infinito, formando um cilindro de altura infinita com centro sendo o eixo , ou .
Então se isolarmos :
Podemos pegar a variação como sendo:
Agora analisando as outras equações
A outra restrição é o máximo valor de na equação , que acontece quando , onde , então no plano temos:
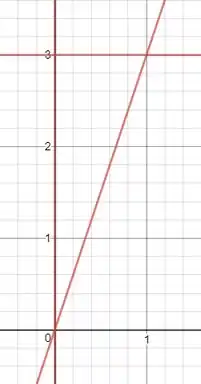
Podemos botar a variação como sendo
Então nossa integral se torna:
Vamos lembrar de prestar atenção na ordem de integração, como temos o valor de dependento do valor de , vamos integrar primeiro em , depois como o valor de depende do valor de , então temos que integrar em !
Passo 2
Resolvendo a integral começando pelo , temos:
Fazendo a substituição dos intervalos de integração:
Voltando a nossa integral, ficamos com:
Passo 3
Agora calculando a integral em :
Fazendo a substituição do intervalo de integração:
Vamos retornar essa coisinha feia do pai pra integral:
Passo 4
Integrando em relação a :
Podemos simplificar essa conta colocando o valor em evidência:
Fazendo essa integral:
Aplicando os limites de integração, temos:
Voltando para a integral:
No final, temos o resultado: