Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 22123456789101112131415161718192021232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

  1. Calcule a massa do sólido W , limitado pelas superfícies x 2 + y 2 = 1 , z + y = 2 e z = 0 , se a densidade é dada por ρ x ,   y ,   z = z .

Passo 1

Cara, massa de um sólido a essa altura do campeonato para a gente não é nada mais é do que uma integral tripla

M a s s a W = ∭ W ρ x ,   y ,   z d V

Onde já temos a função de densidade ρ x ,   y ,   z = z . Mas aí surge uma duvida:

  • Quem é o sólido W que estamos trabalhando?

Passo 2

Vamos começar aqui respondendo a primeira pergunta!

Bem, se você quer entender o sólido, desenhe como sempre fazemos, essas superfícies delimitadoras juntas no espaço obtendo esse carinha aí oh!

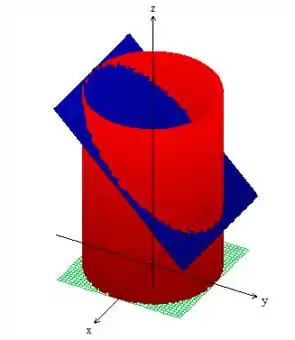
Passo 3

Pow! estamos dentro de um cilindro, então nada mais justo que pensarmos na mudança para coordenadas cilíndricas, certo? Então aqui la vai a troca

x = r cos ⁡ θ  

y = r sin ⁡ θ

z = z

O J a c o b i a n o dessa mudança é

J = r

Como sempre, só terminamos uma troca depois que verificamos onde cada um desses novos termo ( r ,   θ   e   z ) variam!

Passo 4

No caso, r é bem easy de se encontrar, afinal de contas ele é o cara que está variando da origem até a casca do cilindro vermelho:

0 ≤ r ≤ 1

θ , easy também, pois como ele gira ao redor do eixo z no plano x y , vemos que ele precisa dar uma volta completa, logo

0 ≤ θ ≤ 2 π

Em relação a ultima variável, o z , perceba que ele varia de uma base até um teto:

B a s e ≤ z ≤ T e t o

P l a n o   v e r d e ≤ z ≤ P l a n o   a z u l

como o plano azul é z + y = 2 ...

0 ≤ z ≤ 2 - y

Sim, estamos em outras coordenadas agora, então

0 ≤ z ≤ 2 - r sin ⁡ θ

Passo 5

Bem, agora é só montar a integral tripla e correr para o abraço!

∭ W   ρ ( x ,   y , z )   d V

Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo J a c o b i a n o ;)

∫ 0 2 π ∫ 0 1 ∫ 0 2 - r sin ⁡ θ z   J   d z d r d θ =

∫ 0 2 π ∫ 0 1 ∫ 0 2 - r sin ⁡ θ z   r d z d r d θ

Calculando essa integral aí então começando pela de dentro em z , portanto considerando todos uma constante...

∫ 0 2 π ∫ 0 1 r ∫ 0 2 - r sin ⁡ θ z d z d r d θ =

∫ 0 2 π ∫ 0 1 r z 2 2 0 2 - r sin ⁡ θ d r d θ =

∫ 0 2 π ∫ 0 1 r 2 - r sin ⁡ θ 2 2 d r d θ =

simplificando um pouco

∫ 0 2 π ∫ 0 1 r 4 - 4 r sin ⁡ θ + r 2 sin 2 ⁡ θ 2 d r d θ = ∫ 0 2 π ∫ 0 1 2 r - 2 r 2 sin ⁡ θ + r 3 sin 2 ⁡ θ 2 d r d θ =

e agora integrando a de dentro

∫ 0 2 π ∫ 0 1 2 r - 2 r 2 sin ⁡ θ + r 3 sin 2 ⁡ θ 2 d r d θ =

∫ 0 2 π r 2 - 2 r 3 3 sin ⁡ θ + 1 2 r 4 4 sin 2 ⁡ θ 0 1 d θ =

∫ 0 2 π 1 - 2 3 sin ⁡ θ + 1 8 sin 2 ⁡ θ d θ =

Lembrando que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 …

∫ 0 2 π 1 - 2 3 sin ⁡ θ + 1 8 1 2 - cos ⁡ 2 θ 2 d θ = ∫ 0 2 π 17 16 - 2 3 sin ⁡ θ - cos ⁡ 2 θ 16 d θ =

17 16 θ + 2 3 cos ⁡ θ - 1 16 sin ⁡ 2 θ 2 0 2 π =

chegamos ao resultado !

17 16 2 π = 17 π 8

Resposta

17 π 8

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )