Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 43123456789101112131415161718192021222324252627282930313233343536373839404142444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Coordenadas Cilíndricas

Seja a > 0 .

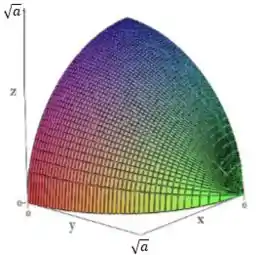
Considere a região compacta V do espaço, onde V = x , y , z ∈ R 3     x 2 + y 2 + z 2 ≤ a ,   z ≥ 0 } .

Considere a integral tripla:

I = ∫ ∫ ∫ V z cos ⁡ x 2 + y 2 d x d y d z

  1. Expresse I na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas r , θ , z (Neste item não é pedido o cálculo da integral).
  2. Calcule I , em termos de a .
  3. Seja W = V ∩ x , y , z ∈ R 3     x ≥ 0 , y ≥ 0 } . E, seja:

J = ∫ ∫ ∫ W z cos ⁡ x 2 + y 2 d x d y d z

  1. Esboçe W .
  2. Encontre o número real c , tal que J = c I .

Passo 1

Vamos inicialmente fazer um esboço da região V , pra ficar mais fácil de visualizar o problema. V é o hemisfério superior de uma esfera centrada na origem e de raio a .

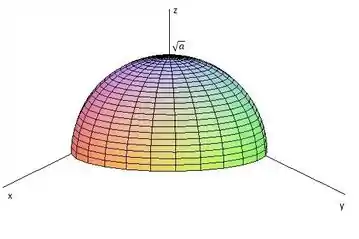
Passo 2

Vamos agora descrever essa região V em coordenadas cilíndricas, pelo “método das fatias horizontais”. As coordenadas r , θ , z variam assim:

0 < r < a - z 2

0 < θ < 2 π

0 < z < a

Pois repare que de acordo com a equação da esfera: x 2 + y 2 ≤ a - z 2 . E como x 2 + y 2 = r 2 , temos que: r ≤ a - z 2 .

Passo 3

Então trocando as variáveis de acordo com a mudança: ( x = r cos ⁡ θ ,   y = r sen ⁡ θ ,   z = z ) :

I = ∫ 0 a ∫ 0 2 π ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d θ d z

Não esquecendo de colocar o r nos elementos infinitesimais.

Passo 4

Resolvendo a letra b)

Usando a integral encontrada no item anterior, vamos calcular!

I = ∫ 0 a ∫ 0 2 π ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d θ d z

I = 2 π ∫ 0 a ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d z

Escolhendo a substituição u = r 2 , teremos d u = 2 r   d r   →   d u 2 = r   d r .

E com essa substituição, se 0 < r < a - z 2 , então 0 < u < a - z 2 , pois u = r 2 .

Logo:

I = 2 π ∫ 0 a ∫ 0 a - z 2 z cos ⁡ u d u 2 d z

I = π ∫ 0 a ( sen ⁡ a - z 2 - sen ⁡ 0 )   z   d z

I = π ∫ 0 a sen ⁡ a - z 2 - 0 z d z

I = π ∫ 0 a z sen ⁡ a - z 2 d z

E escolhendo agora a substituição

t = a - z 2

teremos

d t = - 2 z   d z   →   - d t 2 = z   d z

Com essa substituição, temos, no limite inferior

z = 0 → t = a - 0 2 = a

No limite superior

z = a → t = a - a 2 = a - a = 0

Então

a < t < 0

Logo:

I = π ∫ a 0 sen ⁡ t   - d t 2

I = π 2 ( cos ⁡ 0 - cos ⁡ a )

Passo 5

Resolvendo a letra c)(i)

Um esboço pra W é:

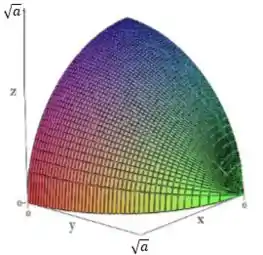
Que só toma a parte da figura com x , y , z ≥ 0

Passo 6

Resolvendo a letra c)(ii)

Como temos:

I = ∫ 0 a ∫ 0 2 π ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d θ d z

e

J = ∫ ∫ ∫ W z cos ⁡ x 2 + y 2 d x d y d z

Vamos escrever a integral J nos extremos da região W :

J = ∫ 0 a ∫ 0 π 2 ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d θ d z

Colocando os extremos de θ pra fora da integral, teremos então que:

I = 2 π ∫ 0 a ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d z

e

J = π 2 ∫ 0 a ∫ 0 a - z 2 z cos ⁡ r 2   r   d r d z

Ou seja, verificamos que a integral I é igual a 4 vezes a integral J :

I = 4 J   →     J = 1 4 I

A constante c vale 1 4 .

Resposta

a )   I = ∫ 0 a ∫ 0 2 π ∫ 0 a 2 - z 2 z cos ⁡ r 2   r   d r d θ d z

b )   I = π 2 ( 1 - cos ⁡ a )

d )   c = 1 4

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )