Considere o sólido que está dentro da esfera , acima do plano e abaixo do cone . Calcule o volume de utilizando coordenadas:
(a) Cilíndricas.
Passo 1
Bom, vamos começar entendendo o que a gente está estudando.
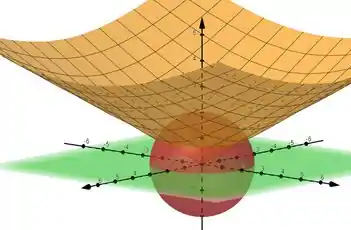
A interseção entre a esfera e o cone é uma circunferência . Quando levada até o plano xy, forma um cilindro que vou plotar de azul pra você enxergar comigo.
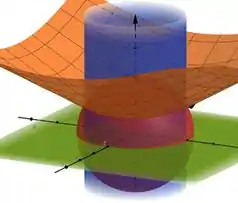
Assim percebemos que o esboço do sólido seria o que está por dentro do cilindro e abaixo do cone, mais a parte de fora do cone, até encontrar a esfera.
Passo 2
Nas coordenadas cilíndricas, analisando o cilindro que se forma abaixo da interseção da esfera com o cone (que está de azul na imagem).
Agora observando nossos intervalos, o r varia de zero até , dá a volta completa, o que seria de zero a , e o z vai de zero até a função do cone, que é então
Passo 3
Analisando a parte que está dentro da esfera, mas não dentro desse cilindro, vemos que o raio vai variar do valor máximo do cilindro () até a periferia da esfera, 2. O ainda da uma volta completa (0 a ), seu z vai variar de zero até a esfera. Isolando z então
Colocando tudo no papel ficamos com