UFABC-Função de várias variáveis - Lista 7 integrais triplas
Utilize as coordenadas cilíndricas
e calcule as integrais dadas a seguir, utilizando a formula da mudança de variáveis:
Onde
onde R é a região contida dentro do cilindro e , entre os planos z=0 até z=x+y+3
Passo 1
Bem pessoas, essa é uma questão padrão de integração tripla. Ele não deu a integral bonitinha, então precisamos desenhar o domínio de integração, para após resolver utilizando a mudança de coordenadas para as cilíndricas.
Mas como resolver? Bem, para resolver precisaremos de alguns conceitos de matemática básica e também de conceitos de integração.
Você lembra deles?
CAAAAAAAAAAAAALMA, se lembrar ótimo. Caso contrário vamos resolver aqui passo a passo com você para você aprender certinho belezinha?
Então vaaaaaaaaaaaamos lá
Passo 2
Analisando os cilindros nos vemos que eles tem um raio igual a 3 e o outro tem um raio igual a 2 e crescem infinitamente ao longo de z.
Porém ele é cortado por 2 planos, então o desenho disso deve ser algo mais ou menos assim:
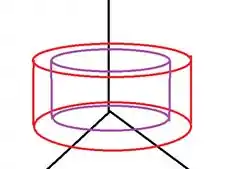
Então nossa integralzinha deve ficar uma circunferência no plano e vai crescer entre esses dois planos , logo nossa integral ficará:
Meu boy, como temos uma circunferência completa de raio variável vamos utilizar a seguinte transformação cilíndrica:
Com e nosso raio é , substituindo tudo na integral temos:
Passo 3
Como os limites de integração depende das variáveis, é importante definir a ordem que você integra. Então vamos de dentro para fora só para manter a metodologia.
Integrando o eixo temos que:
Agora vamos realizar a distributiva e integrar o eixo , mas lembrando o é uma constante em relação ao
Para resolver essa integral precisaremos de duas identidades trigonométricas:
Substituindo nas integrais e as resolvendo, chegamos na solução que é