Use integração tripla em coordenadas cilíndricas para calcular o volume do sólido delimitado pelas superfícies e .
Passo 1
Cara, vamos entender que região é essa. Temos essa equação
Como a gente tem dois termos ao quadrado somados de um lado e um termo ao quadrado do outro lado, a gente entende que isso é um cone, e ele passa pela origem (só ver que o ponto satisfaz a equação dele).
Já a outra
Ela parece muito com a equação de uma esfera, né? Mas repara que o termo está negativo. Isso mostra que isso não é uma esfera, mas um hiperboloide de uma folha (aquele que parece um tronco de árvore). E o eixo dele é o .
Colocando essas duas coisas num gráfico, para ter uma ideia da região que a gente quer o volume
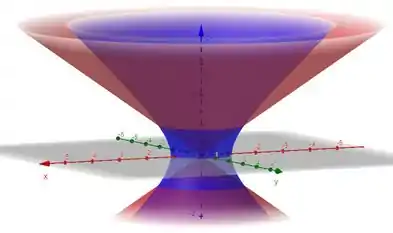
O volume limitado por essas duas superfícies ao mesmo tempo é a região que está fora do cone (essa superfície vermelhinha) e dentro do hiperboloide (a azul).
E repara que a região é simétrica em relação ao plano , então a gente só precisa calcular o volume da parte de cima desse plano e multiplicar por .
Já que a gente sacou isso, bora entender como aplicar as coordenadas cilíndricas aí!
Passo 2
A gente tem que descrever essa região, acima do plano , que vamos chamar de nosso domínio .
Mas a gente vai descrever essa região por coordenadas cilíndricas. Isso significa que a gente vai aplicar as transformações:
Então para escrever os extremos de integração, limitamos essas variáveis que a gente tem: e .
Vamos começar observando a variável . Nesse eixo, vemos que nossa região está entre o plano , ou seja, e a altura onde nossas superfícies se interceptam.
A gente pode tentar achar que valor de é a partir das nossas equações:
Da primeira equação
E voltando para a segunda
Como nossa altura está acima de , podemos dizer que nosso valor é .
Então podemos escrever:
Passo 3
E e ? A gente sabe que é o segmento que sai da origem. Então para limitar ele, vamos pensar assim: vimos que nossa região está dentro do hiperboloide. Isso significa que nosso só pode ir até essa superfície. Logo, ela limita o valor máximo desse segmento. Então vamos escrever
E a gente também viu que a nossa região está fora do cone. Isso significa que o tamanho do nosso , para percorrer nossa região, precisa ser maior que o cone. Então vamos escrever:
Agora a gente precisa das expressões do cone e do hiperboloide em função de e (nossas novas variáveis, além de ) para colocar ali, né? Cara, aqui a gente vai ter que substituir as nossas expressões da mudança de coordenadas nas nossas equações das superfícies, e isolar .
- No cone
Como é sempre positivo, não precisamos nos preocupar com a parte negativa da raiz que tiramos ali.
- No hiperboloide:
Agora a gente pode substituir essas expressões no nosso raciocínio ali
E como não há mais restrições ou equações, podemos assumir:
Belezinha?
Passo 4
Agora é montar a integral. Para calcular o volume precisamos calcular a integral tripla de . Nosso domínio é . Mas vimos que isso é a metade da nossa região. Então precisamos calcular:
Mas essa integral está em e precisamos mudar ela para . Vamos multiplicar o integrando por :
Aí a gente pode colocar nossos extremos de integração:
Como está entre funções, precisamos integrar em relação a ele primeiro.
Passo 5
Bora calcular essa belezura:
Conseguimos!