UFJF. Cálculo 3. Lista de Estudos. Lista da AV1 – 2022.2. Questão 4a.
4. Seja o sólido interior ao cone abaixo do plano e considere a integral
a) Forneça uma expressão para em coordenadas cilíndricas.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, foi dado um solido que é obtido pela parte interna do cone e abaixo do plano .
A partir dessa região, temos que calcular a integral em que
Em coordenadas cilíndricas.
Lembra como fazemos isso? 🤔🤔
Quando temos um sistema de coordenadas e temos que converter esse sistema para coordenadas cilíndricas , temos que reescrever e de outra forma.
No caso, e . Dessa forma, quando temos , em cilíndricas temos , ou seja, .
Mas antes, vamos começar o problema visualizando o solido .
Bora lá? 😁
Passo 2
é delimitado por e . Isolando na primeira equação, temos
Se esboçássemos os gráficos dessas equações, íamos obter algo parecido com
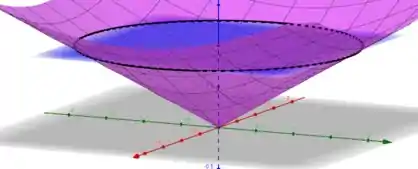
Nessa imagem, vemos que varia de a e como o cone está centrado na origem que faz uma volta completa nesse ponto, a variação de é de a .
Mas e ? Varia de quanto a quanto?
No ponto máximo, , se como dizemos antes, então
Ou seja, quando está em seu valor máximo.
Já no ponto mínimo de , é em , que é justamente na pontinha do cone
Assim, vemos que varia de a na nossa integral.
Tranquilo até aqui? 😉
Passo 3
Montando a nossa integral, temos , onde é o jacobiano que não podemos esquecer quando fazemos essa transformação de coordenadas.
Aplicando os limites de integração que obtemos no passo anterior e simplificando a função de integração, temos
Já podemos converter o limite inferior de para cilíndrica também
Como não temos para integrar, se comporta como uma constante, então a integral de uma constante é dada por...
Aplicando os limites de integração
Substituindo esse resultado em
Interessante, não é? 😎
Passo 4
Agora integrando com relação a , vamos aplicar o método de integração polinomial.
Aplicando os limites de integração de , temos
Simplificando e fazendo
Substituindo esse resultado em
E como é uma constante, a integral de uma constante é dada por
Aplicando os limites de integração
Com isso, vemos que nossa integral , dado os limites do solido , resulta em
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
