Considere as constantes positivas e com e:
Seja a integral tripla
a) Para esboce o desenho de . Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas . Não é necessário calcular a integral!
b) Para , calcule em função de .
Passo 1
a) Odeio quando colocam essas constantes. Cara, botava , , , qualquer coisa... mas enfim, vamos lá XD
Bom, só o que precisamos fazer é analisar cada desigualdade do conjunto de pontos , né? Vamos à primeira:
Isso aí é uma esfera de raio , certo? Temos , e , todos ao quadrado, com sinais positivos e mesmo denominador para cada variável! Show, então, até agora sabemos que está na parte interior à esfera, pois o sinal é de .
Vamos para a segunda desigualdade:
Ela nos diz que, dada a esfera da primeira desigualdade, estamos apenas no hemisfério cujo é maior ou igual a !
Seguindo para a terceira, temos:
Opa, agora, além da restrição do ser maior ou igual a , temos a mesma restrição para o ! Assim, estamos, agora, não em um hemisfério dela, mas no primeiro octante!
Finalmente, para a última restrição, teremos:
Ela nos diz que, dessa calota no primeiro octante, ficamos apenas na parte entre e para o eixo . Ou seja, se for menor do que , então estamos fatiando essa calota com um plano . Para o caro de , teremos a calota, bonitinha, como era pra ser ;)
Passo 2
Agora, vamos esboçar essa bagaça. Pela primeira restrição, tínhamos uma esfera de raio . Pela segunda e terceira, pegamos apenas o primeiro octante. Pela terceira, fatiamos ela por um plano em . Juntanot tudo, temos:
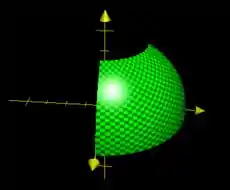
Esse esboço, naturalmente é da superfície de ! Lembre que, como se trata de um volume, é tudo que está dentro dessa parte da esfera. Perceba que na parte de cima, como , não vamos até o final da esfera ;)
Passo 3
Show! Com esse desenho, fica mais simples de montar a integral, né? Os limites de já estão no enunciado, ele varia entre e . Os limites de vemos pela figura: como e são maiores ou iguais a , então está entre e . Agora vem o raio... ele não está entre constantes né? Como estamos em coordenadas cilíndricas, para cada nível , teremos o raio variando de até um certo valor.
Que valor é esse? Veja, se , então temos o raio variando entre e , certo? Se subirmos um pouco, para , então teremos que fazer um Pitágoras para saber esse raio. Sabemos que, para qualquer ponto da superfície da esfera, a distância entre o ponto e a origem é o raio dela, . Então, montamos um triângulo com esse ponto qualquer, a origem e a altura :
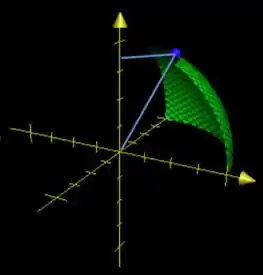
E, então, o raio será:
Show? E, como estamos integrando um volume, ele varia de a
Colocando todos os limites, e o jacobiano da mudança cilíndrica, temos:
Colocando , , das coordenadas polares, temos:
Passo 4
b) Beleza, agora só resolver essa integral! Usando que e colocando , teremos:
Integrando em relação a , temos
Integrando em relação a , temos:
Como ,
Agora, só fazer a distributiva, elevar ao quadrado, e integrar em relação a :D
E aí está, a resposta, a integral é !
Resposta
a) 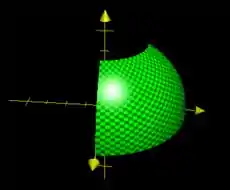
b)