(Capítulo 15.7 – Exercício 23)

a) Expresse o volume da cunha no primeiro octante que é cortada do cilindro pelos planos e como uma integral tripla.

b) Utilize a Tabela de Integrais (nas Páginas de Refêrencia 6-10) ou sistema de computação algébrica para determinar o valor exato da integral tripla da parte (a).

a) O volume de um sólido expressado com integrais triplas é assim:

Mas vamos lá analisar o nosso sólido: temos que, no primeiro octante, a variação de é de até o cilindro, isolando na equação

No primeiro octante pegamos a parte positiva só, então temos .

O vai variar entre o plano e , então

E por fim, o ponto máximo de é quando no cilindro:

No primeiro octante, usamos

Levando isso em conta, a variação de , como tem como valor máximo em , sua variação é .

A integral fica então

b) Showw, agora que já temos a integral, vamos calcular

Focando agora só na integral

Substituindo

Substituindo

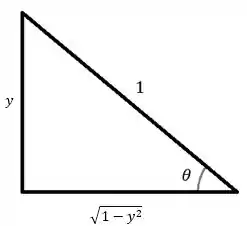
Para voltarmos para a variável , vamos usar o triangulo

Então temos que, pela substituição e pelo triangulo , logo

Então temos que

Usando agora a pagina de referencia

E a outra integral conseguimos fazer por substituição

Substituindo ,

Então temos

Temos que

Ufaaa, acabamos!!