Questão 2:
Seja a região de no quadrante , , entre as superfícies cujas equações implícitas são , , e abaixo da superfície cuja equação implícita é .
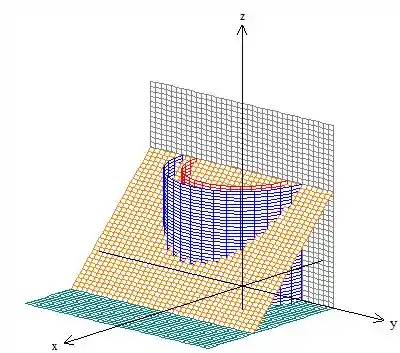
- Faça um esboço de .
- Calcule o volume de .
- Seja a região de que é a união de e a reflexão de no plano , ou seja: é a região acima da superfície , abaixo das superfícies e , e entre as superfície e . Calcule a integral tripla:
Passo 1
Para começarmos esse problema de esboçar , sempre devemos ir com calma! Veja só, sabemos que estamos na parte onde e ...
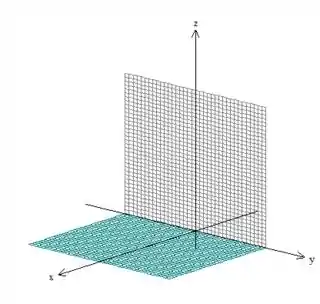
Outra coisa que sabemos também que estamos dentro de dois cilindros de raio e ...
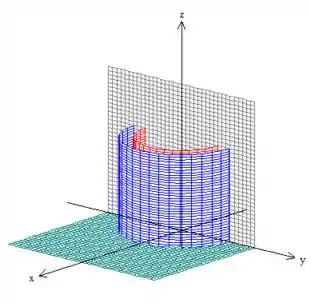
Veja que estamos construindo um sólido!
A outra superfície que também faz parte é o plano , um plano paralelo ao eixo ...
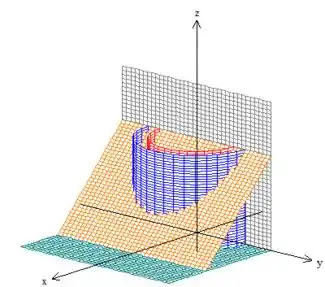
Logo, colocando essas coisas juntas, chagamos ao bom e velho sólido :
Passo 2
Para calcular o volume, o que vamos fazer é calcular uma integral tripla:
Repare que precisamos para retornar a essa integral e matar item descrever região , o que vai ser feita com as coordenadas cilíndricas...
Passo 3
Em toda mudança devemos buscar onde os novos caras, no caso e , estão variando:
Para a variação de e , olhemos para a projeção desse sólido no plano onde essas duas variáveis variam, ou seja, projeção no plano:
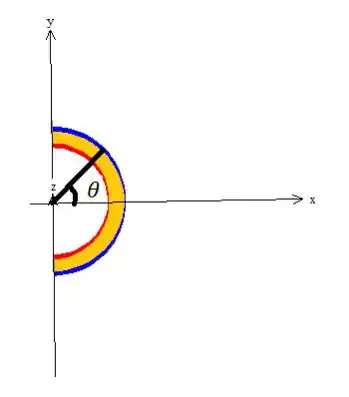
Repare que o raio varia do raio menor até o raio do cilindro maior...
Quanto ao , nessa forma de mudança, ele sempre sai do eixo girando no sentido anti-horário positivo. Como estamos começando antes, o só pode estar girando de...
Para a variação de , repare no sólido que ele é o cara que varia da base, até o teto. Como a base é o plano e o teto, ...
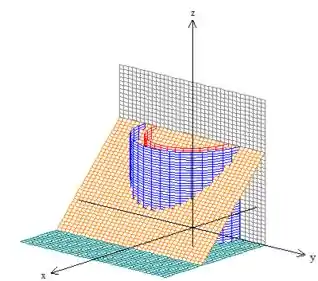
Passo 4
Retornando à integral tripla que queremos resolver...
E substituindo não se esquecendo do Jacobiano...
Resolvendo essa integral de dentro tomando como constante perante
Calculando em ...
E por último em relação a , ganhamos...
Passo 5
Bem, sabemos que a região , é a reflexão da , em torno do plano ...
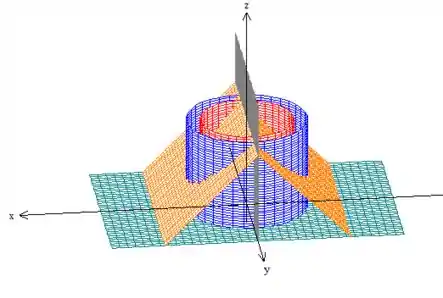
E pretendemos encontrar a solução da integral...
Cara, vou te dar uma ótima notícia. A função , é uma função ímpar em relação ao plano . O que isso significa?
Bem, significa que a função assume os mesmos valores do lá do outro lado do quadrante, mas com o sinal contrário. Por exemplo, pegue o ponto , de tal forma que:
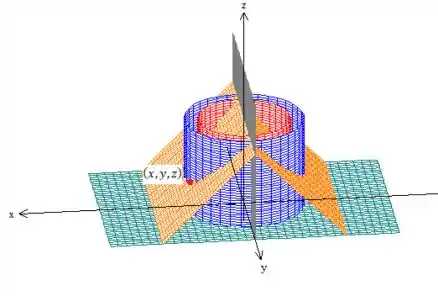
Se pegarmos o ponto simétrico a ele do outro lado do plano ...
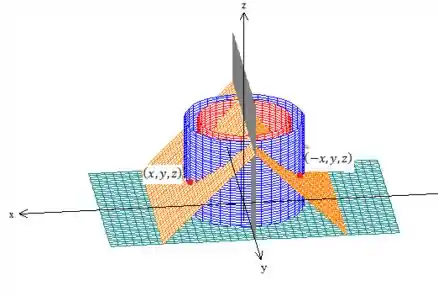
Esse ponto é . Repare que...
Percebeu? Como a região de integração é simétrica em relação ao plano , nem precisamos calcular a integral tripla, pois já sabemos que seu valor nessas condições será...
Resposta