Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 35123456789101112131415161718192021222324252627282930313233343637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Coordenadas cilíndricas

Calcule a integral tripla ∭ B   x 2 + y 2 d V , em que B = { x , y , z : x 2 + y 2 ≤ 1 ,   0 ≤ z ≤ 1 } .

Passo 1

Vamos começar fazendo um desenho da região. Temos um cilindro de raio 1 centrado na origem cortado pelos plano z = 0 e z = 1 :

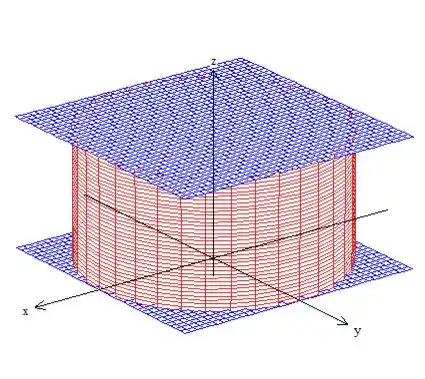
Passo 2

Como temos um cilindro e dois planos limitando nossa região, vamos usar coordenadas cilíndricas. Faremos:

x = r cos ⁡ θ

y = r sen ⁡ θ

z = z

J = r

Passo 3

Vamos, agora, descobrir os intervalos de integração. Como temos uma volta completa em torno do eixo z , sabemos que 0 ≤ θ ≤ 2 π . Pelo próprio gráfico, podemos ver que z varia desde 0 até 1 , logo, 0 ≤ z ≤ 1 .

Já o intervalo de r é desde o eixo z , onde r = 0 até a superfície do cilindro, onde r = 1 , o que podemos tirar da equação:

x 2 + y 2 = 1

Então, podemos escrever a região B como:

B = { ( r , θ , z ) | 0 ≤ r ≤ 1 ; 0 ≤ θ ≤ 2 π ;   0 ≤ z ≤ 1 }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada:

∫ 0 2 π ∫ 0 1 ∫ 0 1 [ r cos ⁡ θ 2 + r   s e n   θ 2 ]   r   d z   d r   d θ =

= ∫ 0 2 π ∫ 0 1 ∫ 0 1 r 3   d z   d r   d θ =

Passo 5

Integrando em relação a z , temos:

= ∫ 0 2 π ∫ 0 1 r 3 z 0 1 d r d θ = ∫ 0 2 π ∫ 0 1 r 3 d r d θ

Passo 6

Agora, integramos em relação a r :

= ∫ 0 2 π r 4 4 0 1 d θ =

= 1 4 ∫ 0 2 π d θ

Passo 7

Finamente, integramos em relação a θ :

= 1 4 θ 0 2 π =

= π 2

Resposta

π 2

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )