Coordenadas cilíndricas
Encontre o volume da região sólida limitada abaixo pelo plano , lateralmente pelo cilindro e acima pelo paraboloide .
Passo 1
Vamos começar desenhando esse sólido, para poder montar o problema. Temos isso aqui:
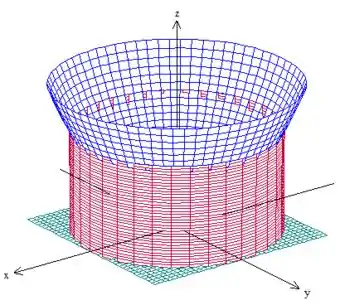
A região do problema é a que fica entre o plano e o paraboloide e é limitada lateralmente pelo cilindro. O volume dessa região é dado por:
Passo 2
Agora vamos escrever matematicamente essa região. Bom, como temos um cone e o sólido tem simetria em relação ao eixo , vamos usar coordenadas cilíndricas, ok? Temos:
Substituindo as coordenadas cilíndricas na equação de cada paraboloide:
Então, como varia entre o plano e o paraboloide, podemos escrever . Como temos uma volta completa em torno do eixo .
Agora falta o intervalo de , que vai desde (no eixo ) até a superfície do cilindro, que tem raio . Portanto .
Assim, a região é a seguinte:
Passo 3
Beleza, agora vamos escrever a integral em coordenadas cilíndricas:
Passo 4
Agora é só resolver isso aí!