Use a integral tripla para encontrar o volume dentro de acima de e abaixo de .
Passo 1
Vamos começar vendo a região que estamos falando. Primeiro, só queremos a parte positiva de , o que está dentro do cilindo e o que está abaixo do paraboloide.
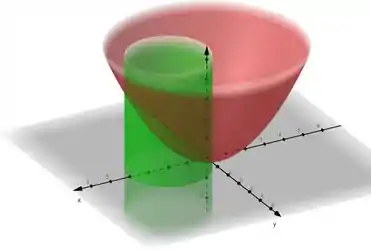
Passo 2
Usando coordenadas cilíndricas, ficamos com
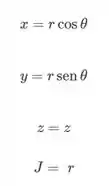
Para a variação do , vamos observar o gráfico acima, e observar que uma varredura do partindo do eixo y negativo () até o eixo y positivo ().
Passo 3
Então beleza, vamos juntar o que a gente tem até agora.
Resposta
Exercícios de Livros Relacionados
Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )