Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 91234567810111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Questão 4. Dado o sólido

E r = x ,   y ∈ R 3   : x 2 + y 2 ≥ r 2 ,   x 2 + y 2 ≤ z ≤ 1

Determinar o valor do parâmetro r   ∈   R tal que o volume de E r seja igual a π 8 .

Passo 1

Bem, sabemos que um volume a essa altura do campeonato é dado para a gente como sendo uma integral tripla:

V E r = ∭ E r   1   d V

Como esse volume é igual a π 8 ...

∭ E r   1   d V = π 8

Perceba então que precisamos substituir os limites de integração no lugar de E r para matarmos o problema. Mas afinal de contas, quem é o sólido E r ?

Passo 2

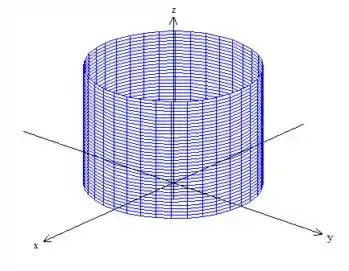
O sólido E r como nos foi dito está pra fora desse cilindro que não conhecemos o raio x 2 + y 2 ≥ r 2 :

z = x 2 + y 2 é um paraboloide:

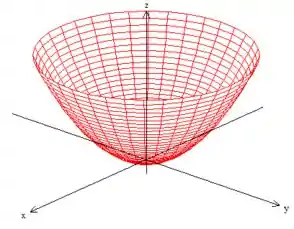
z ≥ x 2 + y 2 representa o interior dele, e não se esqueça que ele vai somente até z = 1 :

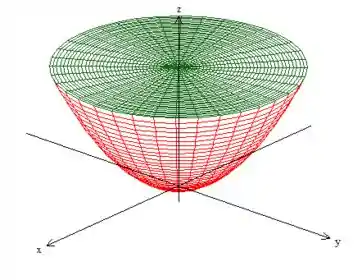
Logo, o sólido E r é esse carinha aqui oh:

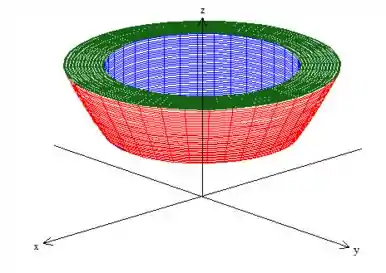
sacou?

Passo 3

Bem, como estamos dentro de um paraboloide e fora de um cilindro, podemos utilizar aqui as mudanças para coordenadas cilíndricas:

x = ρ cos ⁡ θ

y = ρ sin ⁡ θ

z = z

O Jacobiano continua o mesmo:

J = ρ

E uma equação que nos ajuda muito é a equação do próprio cilindro:

x 2 + y 2 = ρ 2

Como sempre, só terminamos uma troca depois que verificamos onde cada um desses novos termo ( ρ ,   θ   e   z ) variam!

Passo 4

No caso, ρ e θ está variando na projeção desse sólido

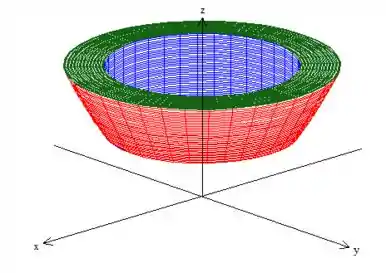
no plano x y :

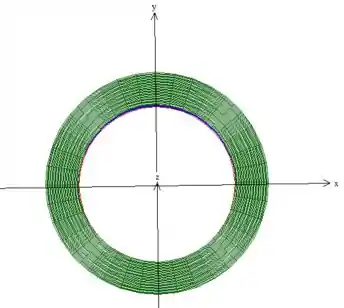
Repare que o raio ρ está variando do raio do cilindro r até o raio máximo que é dado pela intercessão do paraboloide com o plano z = 1 ...

x 2 + y 2 = z     →           x 2 + y 2 = 1

Logo

r ≤ ρ ≤ 1

θ gira ao redor do eixo z no plano x y , vemos que ele precisa dar uma volta completa, logo

0 ≤ θ ≤ 2 π

Em relação a ultima variável, o z , perceba que ele varia de uma base até um teto:

B a s e ≤ z ≤ T e t o

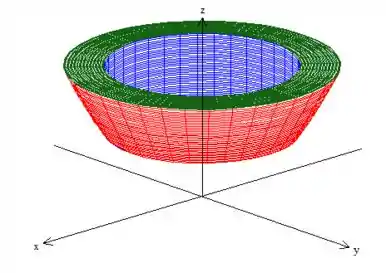
A base é o paraboloide vermelho e o teto é o plano z = 1

P a r a b o l o i d e ≤ z ≤ 1

como o paraboloide é x 2 + y 2 = z ,

x 2 + y 2 ≤ z ≤ 1

Sim, estamos em outras coordenadas agora, então

ρ 2 ≤ z ≤ 1

Passo 5

Voltando para a integral tripla

∭ E r   1   d V = π 8

e tendo em mãos as variações:

ρ 2 ≤ z ≤ 1

0 ≤ θ ≤ 2 π

r ≤ ρ ≤ 1

Podemos substituir as variações na integral (não se esquecendo do Jacobiano) onde vamos obter:

∫ r 1 ∫ 0 2 π ∫ ρ 2 1 1 ⋅ J   d z d θ d ρ = π 8

∫ r 1 ∫ 0 2 π ∫ ρ 2 1 ρ   d z d θ d ρ = π 8

Resolvendo essa integral tripla aí começando pela integral de dentro...

∫ r 1 ∫ 0 2 π ρ ∫ ρ 2 1   d z d θ d ρ =

∫ r 1 ∫ 0 2 π ρ z ρ 2 1 d θ d ρ =

∫ r 1 ∫ 0 2 π ρ 1 - ρ 2   d θ d ρ =

Agora a integral do meio...

∫ r 1 ρ 1 - ρ 2 ∫ 0 2 π   d θ d ρ =

2 π ∫ r 1 ρ 1 - ρ 2 d ρ =

2 π ∫ r 1 ρ - ρ 3   d ρ =

Por fim essa última integral...

2 π ρ 2 2 - ρ 4 4 r 1 =

2 π 1 2 - 1 4 - r 2 2 - r 4 4 =

2 π 1 4 - 2 r 2 - r 4 4 =

2 π 1 - 2 r 2 - r 4 4 =

π 2 1 + r 4 - 2 r 2

Como o volume é igual a π 8 ...

π 2 1 + r 4 - 2 r 2 = π 8       →           1 + r 4 - 2 r 2 = 1 4   →

  r 4 - 2 r 2 + 3 4 = 0

Colocando r 2 = u ...

u 2 - 2 u + 3 4 = 0

Resolvendo por báskara...

u = 2 ± 4 - 4 3 4 2           →               u 1 = 3 2 u 2 = 1 2

Como r 2 = u ...

r 1 = u 1 = 3 2

r 1 = 6 2

Enquanto que...

r 2 = u 2 = 1 2

r 1 = 2 2

Repare que deu 2 resultados, mas se você olhar atentamente para o sólido

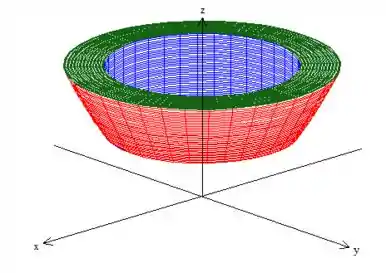
vai perceber que o cilindro que pegamos nas contas é menor que o paraboloide que está dentro de um cilindro de raio 1

Como r 1 = 6 2 e 6 é maior que 2 (pois 2 2 = 4 ), então r 1 > 1 , logo, o raio que queremos só pode ser:

r = r 2 = 2 2

Resposta

2 2

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )