Calcule , onde é o sólido limitado pelas superfícies e .
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido:
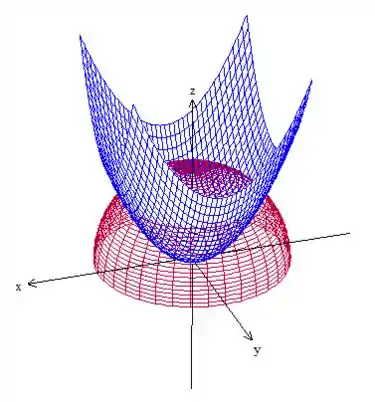
Temos uma semiesfera, pois não podemos ter raiz negativa e um paraboloide virado para cima.
Passo 2
Como o sólido possui simetria em relação ao eixo e as equações que o limitam tem termos quadráticos, vamos usar coordenadas cilíndricas. Faremos:
Passo 3
Vamos, agora, descobrir os intervalos de integração. Substituir esses valores na equação da semi-esfera, temos:
Agora, na equação do paraboloide:
Como os valores de variam entre o paraboloide e a esfera, temos . Pelo próprio gráfico, vemos que , faltam, então, os limites de . Já sabemos que , mas qual o seu valor máximo? Temos esse valor quando as duas superfícies se encontram, certo? Vamos, então, fazer essa interseção:
O que nos dá e , mas, como o ponto não pertence ao paraboloide nem à esfera, sabemos que as superfícies se cortam em . Vamos descobrir, agora, que curva elas formam, substituindo esse valor na equação de uma das superfícies:
Essa é a equação de uma circunferência de raio , portanto, descobrimos que . Então, podemos escrever a região como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Integrando em relação a , temos:
Passo 6
Agora, integramos em relação a :
Passo 7
Finamente, integramos em relação a :