UTFPR– Cálculo Diferencial e Integral I – AVA2 – Questão 3
Uma caixa sem tampa, de base quadrada, deve ser construída de forma que seu volume seja . O material da base vai custar por e o material dos lados por . Encontre as dimensões da caixa de modo que o custo do material seja mínimo
Passo 1
Oi, tudo bem? Essa questão fala em uma caixa de base quadrada e sem tampa que precisa ter um volume de . Foi dado o custo de fabricação e perguntou quais seriam as dimensões que o custo seja mínimo
Puxa, vida e agora? Como encontrar isso?
Quando você tiver questões que perguntem custo mínimo, volume máximo e etc. estamos falando de problemas de otimização!
Normalmente nesses problemas são dados uma informação concreta (no nosso caso o volume da caixa) e uma pergunta algo sobre outro aspecto (no nosso caso o custo)
A ideia para solucionar esse tipo de problema é construir duas equações com as informações e relacionar as variáveis, de forma que você fique apenas com uma variável na função que quer determinar o máximo ou o mínimo
E valos máximo/mínimo se descobre como? Derivando e igualando a zero!
Então é isso! Usando esses passos você encontra tudo que o problema pede!
Mas relaxa, vou fazer com você passo a passo!
Passo 2
Temos uma caixa de base quadrada e sem tampa, então podemos dizer que a aresta da base mede e a altura
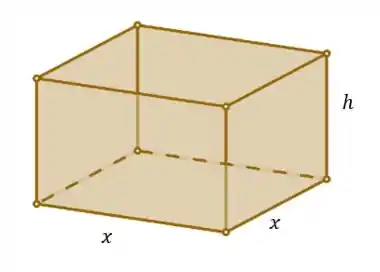
Usa relação entre e ! Perfeito!
Agora vamos ao nosso custo! O valor da base é de por , então vamos relacionar a área da base (e apenas base, não temos tampa!) com esse valor
E as laterais custam por , e temos quatro lados de área :
E agora? Agora vamos construir uma função que dê o custo total dessa caixa (já que é essa quantidade que precisará ser mínima!)
Então temos duas expressões que caracterizam nosso problema
Lembra que o problema pede que o custo seja mínimo, então precisamos derivar a função custo! Para isso acontecer, ela precisa estar em termos de apenas uma variável, então vamos usar a relação que veio do volume para eliminar a altura da função custo
aí temos
Agora nossa missão passou a ser encontrar pontos críticos dessa coisa! E torcer para que seja ponto de mínimo! (vai ser, confia!)
Passo 3
Precisamos derivar a função custo e igualar a zero
agora é só substituir
oba! Achamos!
mas será que esse ponto é ponto de mínimo?
Passo 4
Precisamos verificar se em torno do ponto se a derivada função custo troca de sinal (de negativo para positivo)
Se testarmos a função derivada para, por exemplo, , antes de , vamos ter um valor negativo, e depois, por exemplo , um valor positivo
Isso significa que em temos um ponto de mínimo
Então as dimensões que tornam o custo mínimo são mesmo
E é isso pessoal! Espero ter ajudado! Vamos treinar mais?