Lista de exercícios 9 – Universidade de Brasília– questão 12
Um retângulo deve ser circunscrito em uma semicircunferência de raio 5 metros. Qual é a maior área que o retângulo pode ter e quais as suas dimensões?
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Fica mais fácil se nós fizermos um desenhos. Han?
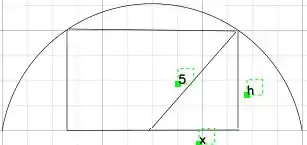
Caso se interesse: foi feito com o IPE editor Latex 😊
Vemos que:
Sendo b = 2x, a base do retângulo.
E isso vai nos ajudar no próximo passo.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim, sabemos que a área de um retângulo é dado por:
Substituindo o valor, temos:
Assim, se queremos achar um ponto no qual uma função é máxima? Deriva a função e iguala a 0, depois ache o valor desse ponto.
Assim:
Igualando a 0:
Passo 3
De forma que:
Assim a área é:
Logo a maior área possível será alcançada quando
Resposta
Exercícios de Livros Relacionados
Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva y = tan x que está mais próximo do ponto ( 1,1 )
Resolva o problema no Exemplo 4 se o rio tiver 5k m de largura e o ponto B estiver somente a 5k m de A rio abaixo.
Encontre o ponto sobre a reta y = 4 x + 7 que está mais próximo da origem.
Se 1200c m 2 de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
Um fazendeiro quer cercar uma área de 15000m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerc