Uma refinaria de petróleo está em na margem norte de um rio reto que tem de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento em na margem sul do rio, a leste da refinaria. O custo de construção do oleoduto é sobre a terra, até um ponto na margem norte do rio é sob o rio até o tanque.
a) Obtenha o custo total de construção do oleoduto, , em função da distância , entre e .
b) Determine os pontos críticos de em .
c) Qual o valor de que minimiza o custo de construção do oleoduto?
Passo 1
Iae, meus queridos! Tudo certinho??

Partiu fazer uma questão bacana sobre otimização que é de praxe em provas de cálculo, mas não se preocupe, vou tentar explicar da melhor forma possível 😁.
Temos os seguintes dados:
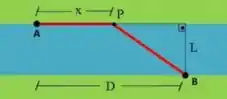
Temos uma refinaria no ponto e temos que construir um oleoduto até o ponto . vale e vale .
Para construir um oleoduto na margem do rio, o custo é de , já sob o rio o custo é , ou seja, é mais barato construir na margem.
Passo 2
No item a) temos que elaborar uma equação que indique o custo de construção do oleoduto quando o valor de poderá variar de a .
Com isso, o custo é dado por
O custo de construção na margem () é mais simples pois é apenas uma linha reta
Já o custo de construção sob o rio () é um pouco diferente. Podemos analisar a distância entre e como sendo a hipotenusa de um triângulo retângulo
Logo será.
Passo 3
No item b) para determinar os pontos críticos de uma função, temos que deriva-la e iguala-la a .
A derivada da soma é a soma das derivadas, então
A primeira é simples
A segunda é mais complicada
Aplicando a regra da cadeia, considerando
Juntando tudo novamente, temos
Para encontrar os pontos críticos vamos igualar essa equação a .
As raízes de são , portanto esses são os pontos críticos da função .
Passo 4
Por fim, no item c), temos que determinar o valor de que faz com que o custo de construção do oleoduto seja o menor possível.
Calculamos os pontos críticos no item b) e encontramos os pontos críticos e , com isso, o menor valor do custo de construção só pode ser quando , já que vai além da distância . Com o valor de encontrado, o custo será
Podemos ver isso graficamente plotando a função no intervalo de a
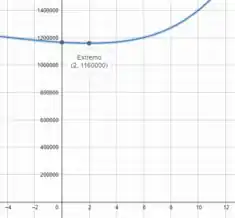
Muito legal né? Entendeu tudo? Responde Aí! 😎👍
Resposta
A)
B)
C) ,