Quais são as dimensões da mais leve lata em forma de cilindro reto, sem tampa, para conter exatamente .
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Bem, temos aí um cilindro sem tampa que será mais ou menos assim:
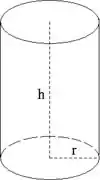
O volume do cilindro será:
O cilindro mais leve será aquele que usa menos material e que, portanto, tem a menor área:
Passo 2
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Não dá para otimizar a função área que a gente tem, pois há duas variáveis. Temos que relacionar uma com a outra antes. Para isso, usamos a expressão do volume:
Substituindo:
Passo 3
Derivamos essa função e achamos os pontos críticos.
Agora derivamos para achar os pontos críticos:
Temos pontos críticos quando a derivada não existe ou é zero.
Ela não vai existir quando , nesse ponto, porém, a área será zero, então a gente esquece isso aí.
A derivada é zero para:
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos ver se esse é um ponto de mínimo mesmo. Um valor à esquerda é e à direita .
Como a derivada é negativa à esquerda e positiva à direita, temos um ponto de mínimo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui, então, próximo passo!
Passo 6
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
O menor valor possível para r é zero. Vimos que nesse valor, a área será nula. Então não consideramos.
O maior valor possível é . Assim:
Dessa maneira, o ponto de mínimo encontrado é global.
Quando tem esse valor: