Problemas de Otimização
As margens de cima e de baixo de um pôster tem e as margens laterais medem cada. Se a área do material impresso sobre o pôster estiver fixa em , encontre as dimensões do pôster com a menor área.
Passo 1
O enunciado pode parecer meio confuso, portanto vamos desenhar para entender o que se passa:
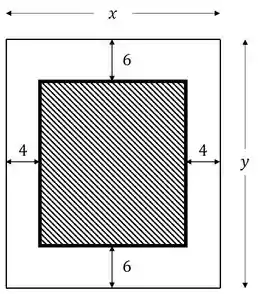
Sejam a largura e a altura do pôster, conforme indicado. Podemos ver que a área impressa é:
Já a área total é:
Que é o que queremos minimizar.
Passo 2
Da equação da área impressa, tiramos:
Portanto queremos o mínimo de:
Passo 3
O mínimo é o ponto onde , logo:
Organizando em quadrados perfeitos:
Passo 4
Como por ser uma medida de comprimento, temos que só o é válido:
Agora precisamos provar que o é um mínimo global. Sim, pois o problema poderia não ter mínimo e a questão ser insolúvel. Vamos por partes. Primeiro provamos que ele é mínimo pelo teste da segunda derivada.
O teste diz que um ponto é mínimo se e somente se . Logo:
Para podemos ver que a derivada é positiva (alias para qualquer ):
Portanto é mínimo. Agora mostramos que ele é global.
Passo 5
Como a função não tende à para nenhum valor , então deve existir um mínimo global. De fato:
Como o único mínimo que existe é , este deve ser então o mínimo global. Portanto as dimensões devem ser: