Um rio tem de largura. Deseja-se estender um cabo de comunicação ligando os pontos e , situados em margens opostas. O ponto está a justante (isto é, rio abaixo) do ponto , conforme a figura.
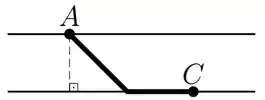
O custo de instalação do cabo é de por metro no leito do rio e de por metro no solo seco. Determine quantos metros de cabo deverão ser instalados no rio e quantos em terra para que o custo total seja mínimo.
Passo 1
Vou redesenhar a figura adicionando as distâncias e um ponto auxiliar :
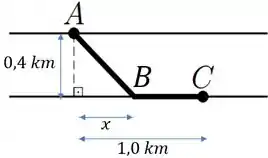
O objetivo é saber que distância de cabo e otimiza o custo, de acordo com os dados. Em resumo, se eu chamar de eesse primeiro ponto na outra margem, e de a distância horizontal de até eu já estou pronto para modelar o problema.
A distância está no rio, e tem seu custo de por metro. Já está na margem, custará o metro. Assim, a função preço seria:
No caso, em função de , são por Pitágoras e por uma diferença simples:
será dado da seguinte maneira:
Passo 2
Agora só precisamos otimizar essa função! Deriva para e iguala a :
Esse é o valor de que otimiza o preço.
O valor do preço otimizado é, então:
Passo 3
Com isso, os valores de (no rio) e (na margem) serão:
Passo 4
E aí... Já acabou a questão??? Nãããooo....Precisamos verificar os valores extremos do nosso domínio onde a função está definida.
Para :
Se fizermos :
Passo 5
Como , temos que é o valor de que otimiza o preço. Portanto, como calculamos no passo 3: