Problemas de Otimização
Determine as dimensões de um cone circular reto de maior volume cuja geratriz tenha de comprimento.
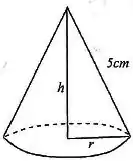
Passo 1
Bom, o volume do cone é dado por:
E nós temos a seguinte relação entre e :
Substituindo na equação do volume nós chegamos a uma função unicamente de :
Passo 2
Vamos agora derivar e igualar a para otimizar a função do volume:
Como a altura não pode ser negativa, achamos que há um ponto crítico em ao substituir a derivada por valores menores que esse e maiores que esse notaremos que a derivada era positiva e depois fica negativa. Esse vai ser um ponto de máximo portanto. Agora basta descobrir o valor de para esse :
Resposta
Exercícios de Livros Relacionados
Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva y = tan x que está mais próximo do ponto ( 1,1 )
Resolva o problema no Exemplo 4 se o rio tiver 5k m de largura e o ponto B estiver somente a 5k m de A rio abaixo.
Encontre o ponto sobre a reta y = 4 x + 7 que está mais próximo da origem.
Se 1200c m 2 de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
Um fazendeiro quer cercar uma área de 15000m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerc