Encontre o ponto sobre a reta que está mais próximo da origem.
Passo 1
Vamos por partes.
O problema pede que achemos o ponto que pertença à reta e que seja o mais próximo possível da origem . Ou seja, temos que minimizar a função distância do ponto até a origem.
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
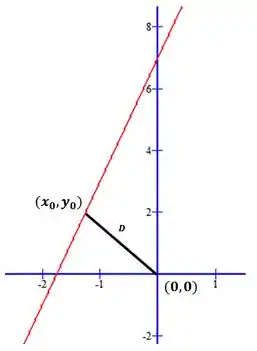
A reta está em vermelho no desenho acima. O segmento de reta preto ilustra a distância de um ponto qualquer da reta e a origem.
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Vale lembrarmos a fórmula da distância entre dois pontos.
Seja o ponto 1 e o ponto 2 . A distância entre eles é dada por:
No nosso caso aqui, temos o ponto e a origem . Aplicando a fórmula da distância:
Outra relação importante é o fato de o ponto pertencer à reta . Portanto:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos minimizar a função distância :
E sabemos que:
Substituindo:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Como a raiz do denominador é positiva por ser uma raiz quadrada, então basta fazermos:
O denominador é sempre positivo, pois não tem raízes reais.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Usando o teste da primeira derivada, podemos ver que para todo e para todo . Portanto, é realmente um ponto de mínimo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a destacar aqui.
Passo 7
As fronteiras para são as fronteiras para a reta, ou seja, e . É fácil notar que quando a reta vai para os extremos, a distância para a origem aumenta cada vez mais. A menor distância, portanto, é o valor encontrado no ponto crítico que será mínimo global.
Resposta
O ponto é .