Um cilindro circular reto é inscrito em uma esfera de raio . Encontre a maior área de superfície possível para esse cilindro.
Passo 1
Ih jovem, o enunciado é curtinho mas essa questão tem cara que vai dar um trabalhão. Enfim, não adianta chorar, mãos à obra!
Vamos começar desenhando a situação e dando nome aos bois (no caso, os bois seriam as variáveis relevantes do problema):
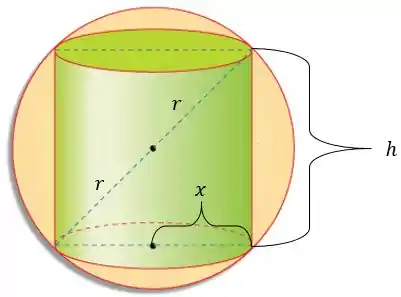
O raio da esfera nós sabemos que é . Além dele, chamei o raio e altura do cilindro de e , respectivamente. Tranquilo?
Passo 2
Ok, agora que deu pra visualizar o problema vamos bolar nossa estratégia.
Ele quer a área lateral máxima possível pra esse cilindro (o enunciado ficou meio ambíguo, porque “área de superfície” poderia incluir a área das tampas, mas enfim, no gabarito oficial ele só fala da área lateral mesmo).
E essa área lateral é dada pelo perímetro do cilindro vezes a sua altura:
Então temos que maximizar essa função!
E o grande lance é que depende diretamente de . Isso dá pra imaginar na figura: quanto mais “gordo” o cilindro, mais baixo ele vai ser. E quanto mais fininho, mais alto na esfera ele consegue ir.
Passo 3
Agora vamos achar a relação entre e .
Pra isso vamos dar uma olhada na figura de frente. Assim, veremos o cilindro como se ele fosse um retângulo. E dentro desse retângulo podemos enxergar vários triângulos retângulos, que nem esse aqui embaixo, saca só:
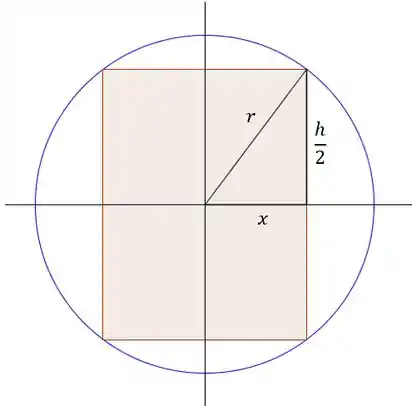
Assim, pelo mais do que clássico Teorema de Pitágoras:
Agora é só isolar o :
(Obs.: é uma altura , então não poderíamos ter .)
Passo 4
Voltando pra expressão da área lateral:
Como é uma função de , podemos escrever , aí fica:
Ah, uma coisa que vale a pena ressaltar é que o domínio dessa função é . Isso porque:
- é o raio de um cilindro, então
- o cilindro está inscrito numa esfera, então seu raio tem que ser menor que o da esfera
Tudo sussa na montanha-russa? Então vamos continuar!
Passo 5
Agora fique à vontade pra esquecer esfera, esquecer cilindro e deixar isso tudo pra depois.
Caímos num problema de maximização de função, que poderia estar num Stewart da vida sem nenhum contexto geométrico. Até aqui modelamos o problema, agora é só conta!
O que queremos é maximizar a função
Pra isso, vamos começar derivando nossa colega com a regra do produto e a regra da cadeia:
Usando que:
Temos:
Passo 6
Beleza, agora vamos zerar essa derivada pra achar os pontos críticos:
Tanto como são positivos, então:
Beleza, esse é o único ponto crítico da .
Passo 7
Pra classificar esse ponto crítico, basta estudar o sinal de nos intervalos e .
Pegando algum bem próximo de , temos:
E sabemos que a derivada só se anula em , ou seja:
Agora vamos pegar algum no lado oposto do intervalo, bem próximo de . Daí vamos ter:
Portanto:
Passo 8
A derivada é positiva até o ponto , e depois disso ela é negativa. Logo, pelo teste da primeira derivada, esse ponto é um ponto de máximo.
E como nos extremos do intervalo, e , vale zero, concluímos que é o ponto de máximo global de no intervalo .
Passo 9
Ok, agora podemos voltar pra geometria.
Dessas contas todas aí chegamos à conclusão que o cilindro com maior área lateral possível tem raio .
E o valor dessa área vai ser dado pela nossa função:
O vai cortar, aí sobra:
E essa é a famosa área que tanto queríamos! ;)