Um campo retangular à margem de um rio deve ser cercado com exceção do lado ao longo do rio. Se o custo do material for de no lado paralelo ao rio e de nos dois extremos, ache o campo de maior área que possa ser cercado com de materiais.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Bom, comecei desenhando esse caso aí:
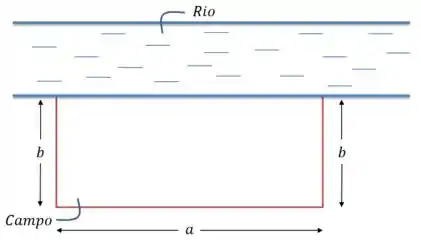
A área do retângulo, que é o formato do campo, vai ser dada por:
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Sendo que temos como limitante aquele preço de . Bom, se custa a cerca do lado paralelo e a dos outros dois, posso criar um custo, estando e em metros, dado por essa equação:
Repara que são dois lados de comprimento e um lado . Como ele diz que esse custo é fixo em , ficamos assim:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Juntando a última equação à da área, tendo colocado o em evidência:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Se eu procuro o ponto crítico da área, ou seja, a maior possível, devo derivar e igualar a esta equação:
Como é um polinômio, a derivada sempre vai existir.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Como a derivada é fácil de calcular, é melhor derivar de novo e aplicar o teste da segunda derivada.
Como a segunda derivada é negativa, esse é um ponto de máximo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não há outros pontos críticos a calcular, então, próximo passo!
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
Olhando para função área:
Vemos que o menor valor para é zero, uma vez que é uma medida. O maior é . Para zero. A área é zero e inútil. Para :
O que também não é aplicável. Dessa maneira é um ponto de máximo global, onde:
Eu sei que é repugnante, mas esse é nosso resultado.