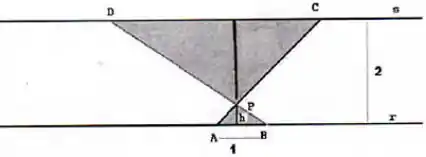
Na figura abaixo, e são retas paralelas, a distância entre elas é , é um ponto fixo de , e são pontos fixos de e a distância entre eles é . É possível encontrar um ponto na reta , de modo que o segmento intercepte e que a soma das áreas dos triângulos sombreados na figura seja mínima? E máxima? Nos casos em que a resposta for afirmativa, encontre a altura do triângulo .
Passo 1
Seguindo os nomes que ele nos deu ali, podemos chamar a altura do triângulo de baixo de e sua base de . A altura do outro triângulo será a diferença entre a distância entre as retas e , ou seja, . Podemos chamar a base do triângulo de cima de . Ora, teríamos a seguinte fórmula para a soma das áreas:
Porém, nessa situação temos duas variáveis na equação, e . Ora, como vincular e ?
Estamos trabalhando com retas paralelas! Isso significa que se uma terceira reta as corta, os ângulos formados com cada uma das duas retas paralelas será igual. Concluímos que o ângulo e o ângulo são iguais, bem como e tem o mesmo valor. Os triângulos, portanto, são semelhantes! Assim, as alturas e as bases deles mantêm a mesma proporção:
Passo 2
Vamos agora derivar o termo e igualar a :
Como não pode ser negativo, o nosso único ponto crítico é . Para determinar se é um ponto de máximo ou mínimo devemos analisar o sinal da derivada antes e depois desse valor de . Ora, é negativo em , não sendo ela definida em , e positivo no resto do domínio. Com isso concluímos que será um ponto de mínimo.
Enfim, resumo da história: temos um mínimo para a soma das áreas em ; não há pontos de máximo.