Encontre as dimensões do retângulo com a maior área que pode ser inscrito em um triângulo equilátero com lado se um dos lados do retângulo estiver sobre a base do triângulo.
Passo 1
Claramente é um problema de otimização. Temos que maximizar a área de um retângulo que pode ser inscrito em um triângulo equilátero, ou seja, que possui três lados iguais.
1º Passo: Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
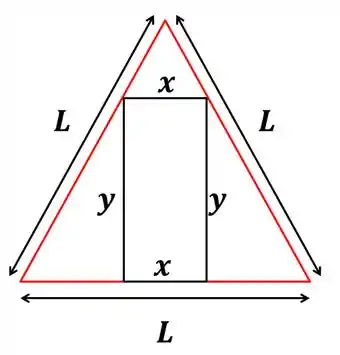
Temos que os lados do triângulo equilátero valem e que os lados do retângulo inscrito valem e .
Passo 2
2º Passo: Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Como relacionar , e ? Vamos desenvolver um pouco mais a figura para encontrarmos uma relação através do Teorema de Pitágoras. Repare:
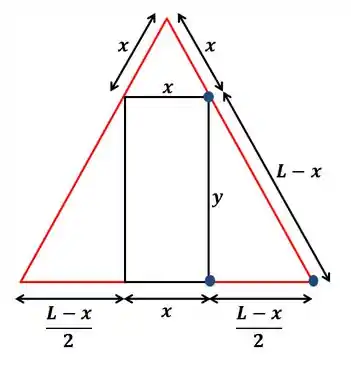
O triângulo formado acima do retângulo também será um triângulo equilátero, já que seus ângulos são de . Portanto, repare que o triângulo formado pelas três bolinhas azuis na figura é um triângulo retângulo e, por isso, podemos aplicar Pitágoras:
Essa é a relação entre e . Lembrando que é um dado do problema. Ou seja, é como se o enunciado tivesse dado quanto vale o lado do triângulo equilátero. ou um número dá no mesmo. O nosso resultado ficará em função de . A área do retângulo é:
Passo 3
3º Passo: Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos maximizar a função área :
E sabemos que:
Substituindo:
Passo 4
4º Passo: Derivamos essa função e achamos os pontos críticos.
Como é um polinômio, a derivada sempre existirá
Passo 5
5º Passo: Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Usando o teste da primeira derivada, podemos ver que para todo e para todo . Portanto, é realmente um ponto de máximo global.
Nem precisamos dos outros passos, já mostramos que é global.
Resposta
As dimensões são e .