Considere todos os triângulos retângulos formados pelos semieixos positivos e por uma reta que passa pelo ponto (2,3). Dentre todos os triângulos possíveis, aquele que possui área mínima tem a hipotenusa valendo:
Passo 1
A área do retângulo será:
Precisamos achar a relação entre e que, por semelhança e triângulos será:
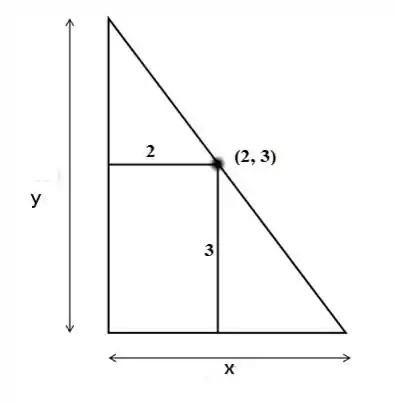
Logo:
Com isso, a área será:
Passo 2
Para achar o máximo, precisamos encontrar os pontos críticos que ficam onde a derivada é zero ou não existe. Então vamos derivar essa sabedoria. Usando a regra da fração:
A derivada não existirá em que será um ponto crítico. Porém, olhe a figura e veja que nesse ponto a inclinação é infinita e área também o será, logo, esse não é ponto que você está procurando!
Zeros também serão pontos críticos e ocorrerão quando:
Multiplicando por -1 dos dois lados...
Então e .
Zero não é legal, pois leva a área . Resta-nos .
Como a questão é de multiplica escolha, não tem porque perder tempo provando que esse é um ponto de mínimo. Como descartamos todos os outros, podemos adotar esse sem medo.
Passo 3
Nesse ponto, vale:
Como e são catetos, a hipotenusa será: