Problemas de Otimização
Encontre os pontos da curva que estão mais distantes do ponto .
Passo 1
Um esboço da situação da distância entre um ponto qualquer na curva até o :
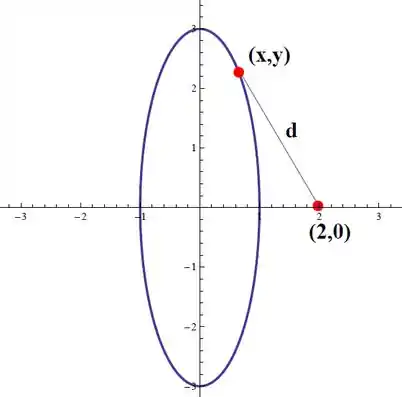
Para simplificar a análise vamos estudar apenas a parte onde , sabendo que a curva é simétrica para baixo, ou seja, se acharmos um par de pontos sabemos que o ponto teria simetricamente a mesma distância até e teria que fazer parte da nossa resposta.
Enfim, para nós temos que seria igual a:
Sendo assim, analisamos a distância entre os pontos e , correto?
Assim, será dado pela raiz da soma dos quadrados das diferenças entre as respectivas coordenadas (espera, o que??). Falando é mais complexo do que é na prática, olha aqui:
Imagina que é a hipotenusa de um triângulo retângulo com os catetos sendo as diferenças entre as coordenadas em e entre as coordenadas em . Aplicamos Pitagoras e chegamos nessa fórmula.
Passo 2
Dada a fórmula, nós podemos otimizar a função se derivarmos em função de e igualarmos o termo a .
Ao observarmos antes e depois de vemos que esse é um ponto de máximo, já que a derivada é positiva antes dele e negativa depois. Assim, o ponto mais distante será o:
Analogamente, temos por simetria que o ponto também é solução para nossa questão, como já havíamos dito no ínicio da questão.