Seja uma reta passando pelo ponto com inclinação negativa. Dentre todos os triângulos retângulos obtidos tomando e a interseção da reta com o primeiro quadrante, encontre as dimensões do que possui a menor hipotenusa.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Esta questão merece um desenho bem feito:
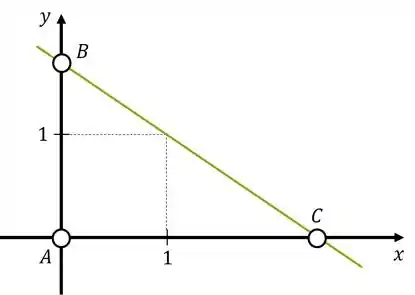
Agora sim podemos começar à pensar. Atribuindo algumas dimensões ao problema
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Repare que existem dois triângulos semelhantes na figura do problema:
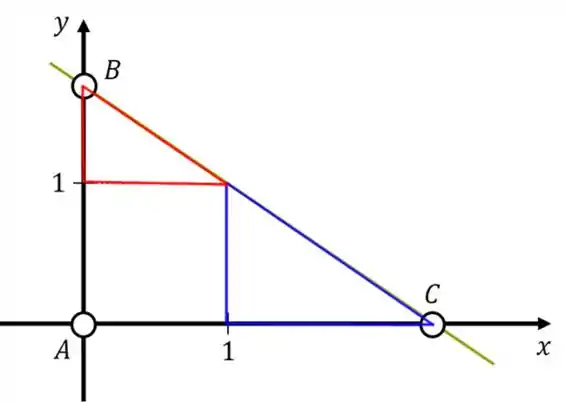
O triângulo em vermelho tem altura e base . O triângulo em azul tem altura e base . Como são semelhantes, podemos usar a semelhança de triângulos:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos achar a menor hipotenusa que será dada por Pitágoras:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Igualando à zero obtemos:
Sumindo com esse denominador que nunca vai poder ser zero ficamos com:
Também teremos outro ponto crítico em que é onde a derivada não existe. Nesse ponto, porém, a reta seria vertical e não tocaria o eixo . Vamos desconsiderá-lo então.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Agora precisamos provar que é um mínimo. Uma alternativa é o teste da derivada segunda, a outra é simplesmente analisar o sinal da derivada . O segundo teste é mais conveniente, pois derivar isso aí de novo seria bem complicado.
Arrumando, podemos ver que o denominador não influencia no sinal. Por ser uma raiz ele deve ser sempre positivo.
Vamos testar um ponto à esquerda e à direita do ponto crítico. Pode ser e . Como o sinal só depende do numerador basta testar somente ele.
Para
Para :
A derivada é negativa à esquerda e positiva à direita, então temos um ponto de mínimo aí!
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Temos um outro ponto crítico em , mas nesse ponto, a reta é vertical e não toca o eixo . A hipotenusa, portanto, será infinita. Maior que nosso ponto de mínimo, obviamente.
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
vai variar desde , que é seu valor mínimo, até infinito. Já vimos o que acontece em . Para :
Como ambas fronteiras vão para mais infinito, garantimos que o nosso ponto de mínimo encontrado é mínimo global!
Resposta
Ei, a resposta está no passo a passo :)