Se é o ponto na curva que está mais próximo de então é:

5. nenhuma das alternativas

Mas o nosso está na curva de equação

Utilizando isso:

Assim a distância ficou só em função de , podemos escrever:

Desenvolvendo essa função distância:

Vamos derivar isso aí pra achar os pontos críticos da função. Pela regra da cadeia:

Agora vamos zerar essa derivada:

Dividindo tudo por :

Hmm... polinômio de 3º grau. Meio chatinho de resolver. Mas enfim lá do pré-cálculo a priori sabemos procurar raízes de polinômios assim. Não vou entrar em detalhes aqui, porque acho que faria a gente perder um belo tempo para algo que foge do escopo da matéria (se você não concorda avisa aí!).

Enfim, temos que:

Então os pontos críticos da função estão em e .

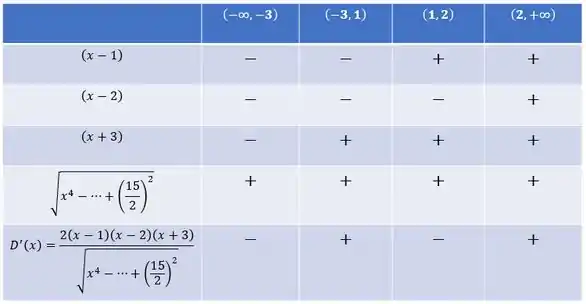
Agora vamos montar um quadro de sinais pra estudar o sinal da derivada.

Vimos que

Então

Aqui está o quadro:

Pelo teste da primeira derivada tiramos que

• é um ponto de mínimo local
• é um ponto de máximo local
• é um ponto de mínimo local

O que nós queremos é o mínimo global, então a disputa esta entre os pontos e . Pra determinar qual é o certo sem muito trabalho, basta usar o bom senso.

Como os pontos estão na curva , esses nossos candidatos são e . Queremos saber quais desses está mais próximo de .

Fica meio óbvio que o ponto está mais perto né? E se não ficar dá pra fazer um esboço grosseiro pra visualizar melhor.

Pode ser bem grosseiro mesmo:

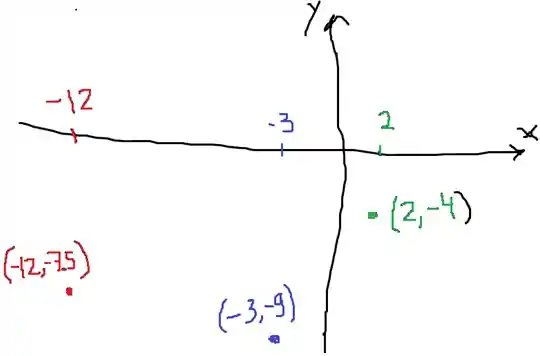
(Não, não foi uma criança de 5 anos que fez esse esboço.)

Então pra concluir: nosso ponto é:

Logo,