Encontre as dimensões do cone circular de maior volume que pode ser inscrito em uma esfera de raio . Calcule o volume desse cone.
Passo 1
Observe a figura abaixo, que representa a situação descrita no enunciado.
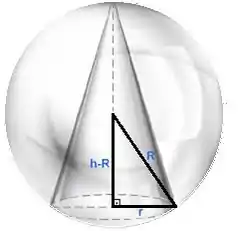
Chamaremos a altura do cone de e o raio de . Queremos as dimensões do cone inscrito de maior volume, que pode ser calculado pela fórmula
Passo 2
Precisamos de uma relação entre as variáveis do cone e o raio da esfera. Essa relação pode ser obtida olhando a figura acima, em que temos um triângulo retângulo cuja hipotenusa é o raio da esfera. Por Pitágoras temos
Portanto
Substituindo na equação do volume temos o seguinte
Passo 3
Agora que possuímos a equação do volume em função de uma das variáveis do cone e do raio da esfera, podemos encontrar seu valor máximo, derivando em função de , achando seus pontos críticos e encontrando o máximo. Mãos à obra.
Os pontos críticos são obtidos igualando a derivada a zero. Então temos:
Passo 4
Show, encontramos como ponto crítico . Mas crítico mesmo é esse momento agora hahah. O que fazer com o ponto encontrado??? Bom, temos que provar que ele é um máximo. Sabemos que a altura do cone está entre 0 e , que é o diâmetro da esfera. Vamos usar o teste da primeira derivada para saber se é de fato um máximo. Temos que analisar o sinal da derivada perto de .
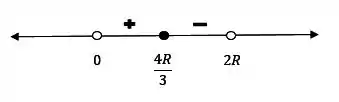
Como a derivada é positiva antes de e negativa após esse ponto, podemos afirmar que esse ponto é um máximo global.
Passo 5
Agora só precisamos achar o valor de e teremos as dimensões do cone de maior volume que pode ser inscrito na esfera. Vamos substituir em
Então
E finalmente podemos calcular o volume máximo do cone inscrito.