Determine o volume do maior cone de revolução que pode ser inscrito em uma esfera de raio .
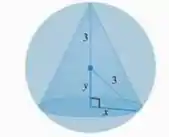
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
O volume do cone estará limitado pelo volume da esfera. A chave para resolvê-lo é relacionar as variáveis dos dois. O volume da esfera será:
O volume do cone, de acordo com as dimensões da figura:
Passo 2
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Para isso, devemos relacionar e . Olhando a figura, vemos que:
Agora é substituir:
Passo 3
Derivamos essa função e achamos os pontos críticos.
Agora derivamos para achar os pontos críticos:
Os pontos críticos estão onde a derivada não existe ou é zero. Sempre vai existir pois é um polinômio. Vai ser zero quando:
As raízes serão e . Não consideramos o valor negativo, pois é uma medida. Vamos ver o ponto então.
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos ver se esse é um ponto de máximo mesmo. Um valor à esquerda é e à direita .
Como a derivada é positiva à esquerda e negativa à direita, temos um ponto de máximo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui, então, próximo passo!
Passo 6
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
O menor valor possível para é zero. Nesse valor, o volume será nulo. Então não consideramos.
O maior valor possível é , que é o raio da esfera. Assim:
Esse também deu zero, então não precisamos nos preocupar com ele.
Para o nosso ponto de máximo:
Comparando com os outros valores, vemos que é um ponto de máximo global.