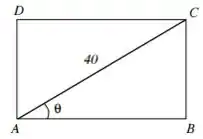
A superfície lateral de um cilindro reto é obtida unindo-se os lados e de um retângulo . Dentre todos os retângulos de diagonal , determine o ângulo (ver figura) que permite construir um cilindro de volume máximo.
Passo 1
Bom, vou precisar de uns conhecimentos de geometria do Ensino Médio para fazer essa. Quando eu abro dessa maneira um cilindro eu reparo que a base do retângulo corresponde ao perímetro da base do cilindro e a altura do retângulo corresponde à altura mesmo do cilindro:
Tendo ainda que o Volume vai valer
A gente consegue escrever em função das distâncias e , saca aqui:
Da mesma, forma, sabemos escrever e em função desse ângulo por trigonometria (lembrando que pela geometria da figura temos apenas entre e ):
Agora vamos derivar essa função para otimizá-la, igualando o a :
Sabemos que se for igual a o volume será nulo, sendo ele ponto de mínimo. Somado a isso o fato de que não podemos graficamente ter dois mínimos seguidos, garantimos que
É ponto de máximo!
OBS.: Vamos lembrar que em problemas de otimização nós também devemos sempre olhar para os extremos do intervalo onde a função está definida. Mas para este nosso caso, já sabemos que se for igual a o volume será nulo, mas também que se for igual a o volume será nulo novamente! Desta forma, nosso é o nosso ponto de máximo!
*Dependendo da forma como você resolve a equação da derivada, o resultado pode ser . Acontece que , então tudo certo =D