Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo, cujo diâmetro é igual à largura do retângulo. Suponha que o perímetro da janela normanda é de .
- Escreva a área da janela como função da altura do retângulo correspondente.
- Aplicando os métodos do cálculo diferencial na função do item (a), ache as dimensões da janela com maior área possível, assim como a área desta janela.
Passo 1
(a)
Vamos começar esboçando essa tal de janela normanda e atribuindo variáveis pras quantidades do problema:
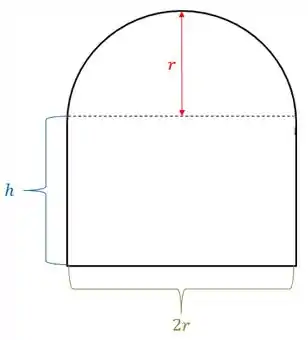
Chamei a altura do retângulo de e o raio do semicírculo de , beleza?
Passo 2
A questão pediu a área da janela, que nada mais é que a área do retângulo mais a área do semicírculo.
Ou seja, chamando a área da janela de , temos:
Passo 3
Mas ela quer a área só em função da altura, então precisamos sumir com esse raio!
A informação crucial que o enunciado deu foi que o perímetro da janela é .
Pela figura, podemos ver que isso vai dar
E o comprimento do semicírculo é simplesmente . Logo,
Passo 4
Ótimo! A gente tinha achado
Então nossa área em função só da altura vai ser:
Passo 5
Vamos só dar uma arrumada nisso aí:
Botando tudo no mesmo denominador :
O vai cortar com , daí fica:
Botando em evidência:
Deu pra ver que essas contas foram bem chatinhas né... As chances de errar são imensas, então é bom ficar ligado! ;)
Passo 6
Pra fechar de vez a letra (a), vamos só definir o domínio dessa função área (acho que não teria problema botar na letra (b), mas o ideal mesmo é fazer isso ainda na letra (a)).
Primeiramente, devemos ter né, porque um retângulo não pode ter altura negativa.
Também temos a restrição que o perímetro da janela é :
Admitindo que , que seria o menor raio possível, isso ficaria:
Então essa é a altura máxima do retângulo. (Obs.: se então a janela tem área igual a zero.)
Portanto, temos que
O domínio da função é o intervalo .
Passo 7
(b)
Agora queremos a maior janela possível.
Então vamos, como sempre, derivar e igualar a zero. Lembrando que:
Derivando:
Pra isso dar zero, devemos ter:
Esse é o único ponto crítico da função.
Passo 8
O valor da área nesse ponto é
Não tá errado não, é esse valor feião mesmo.
Passo 9
Mas antes de afirmar que essa área é a maior possível, temos que conferir também as fronteiras do intervalo: e .
nós vimos lá atrás que vai dar zero (é intuitivo ver pela figura), mas também não custa conferir:
Ok, confirmado.
Passo 10
Então nos restaram 2 candidatos:
Agora fica aquela dúvida, qual valor é maior?
Relaxa que tudo vai dar certo... Repara aqui comigo:
Então:
Beleza? Isso é ótimo, porque assim os valores que queremos comparar são:
Temos que
Ou seja:
Show!! Daí concluímos que a altura do maior retângulo é
E a área desse retângulo é
Passo 11
Antes de sair comemorando, tem o detalhe que ele pediu as dimensões, ou seja, também temos que informar o valor do raio:
Depois desse trabalhão todo, dá vontade de deixar assim mesmo, mas vamos manter a calma (e a classe) e simplificar esse cara:
Cortando o em cima e embaixo:
AGORA SIM! PODE SOLTAR O GRITO!

Resposta
(a)
(b)
Dimensões:
Área máxima: