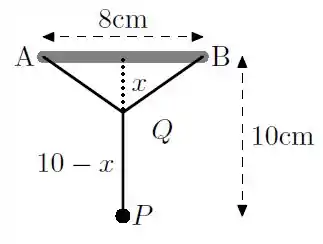
Um peso deve ser mantido suspenso a de uma barra horizontal de extremidades e , por um fio na forma de (veja na figura). Sabendo que o segmento mede , qual o fio de menor comprimento que pode ser usado?
Passo 1
Essa questão facilitou nossa vida: ela já veio com desenho e ela já chamou de a distância do ponto ao ponto médio da barra.
Olhando a figura, podemos ver que o comprimento do fio é a distância de até , mais a distância de até , mais a distância de até :
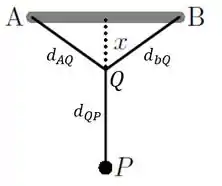
Você concorda comigo que, pela simetria do problema:
Além disso:
Ou seja:
Então só nos resta achar esse pra obter uma expressão pro comprimento do fio.
Passo 2
Esse vai ser tranquilinho de achar, simplesmente por Pitágoras:
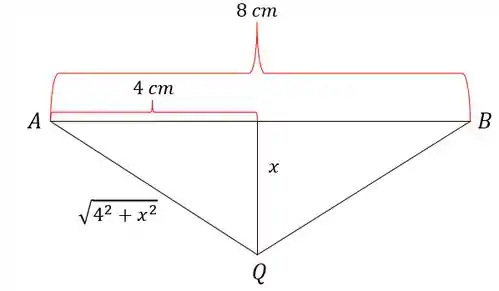
Ou seja,
Assim, o comprimento do fio é:
Detalhe que sabemos que .
Passo 3
Queremos minimizar essa função, então vamos derivar:
Igualando a zero pra achar os pontos críticos:
Como , isso dá:
Esse é o único ponto crítico da função .
Passo 4
Resta só provar que ele é mesmo um ponto de mínimo. Vejamos o sinal da derivada pra e . (Obs.: )
Pra
Pra :
Ou seja, para e para . Então é o ponto de mínimo global de .
Passo 5
Então o menor fio tem comprimento