Seja uma reta que passa pelo ponto e forma um triângulo com os eixos coordenados positivos. Determine a equação de para que área desse triângulo seja mínima.
Passo 1
A situação da questão é essa aqui, ó:
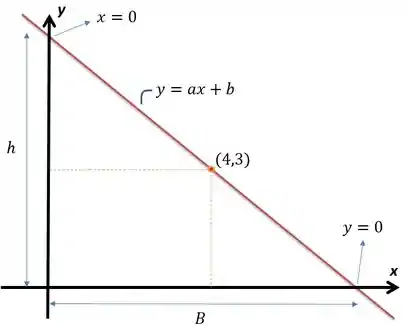
Onde a área do triângulo seria dada por
Agora, como determinamos e em parâmetros da reta? Reparou que eu marquei ali onde e onde ? São pontos que delimitam essas dimensões, assim, a gente vai determinar da seguinte maneira:
Logo,
Só que não vamos conseguir otimizar (no caso, minimizar) uma função com duas variáveis. Como relacionar e ?
A reta passa em ! Isso vai gerar uma relação entre os coeficientes da reta:
Dessa forma:
(a gente percebe na função que o domínio é )
Vamos otimizar!
Passo 2
Derivamos em função de e igualamos a para descobrir o que gera a menor área:
Igualando a , temos:
Se notaremos que não há área delimitada entre os eixos no lado positivo, o que não é útil para nós. Enfim, o valor que a gente procura é .
Para provar que esta é a área mínima, basta fazer:
O que, somado ao fato de que não existem outros pontos críticos (onde ) no intervalo , garante que esse é um mínimo.
Agora, ele não quer a área, ele quer a reta que concede a maior área! Assim, vamos calcular a reta sabendo que ela passa em :
Logo,